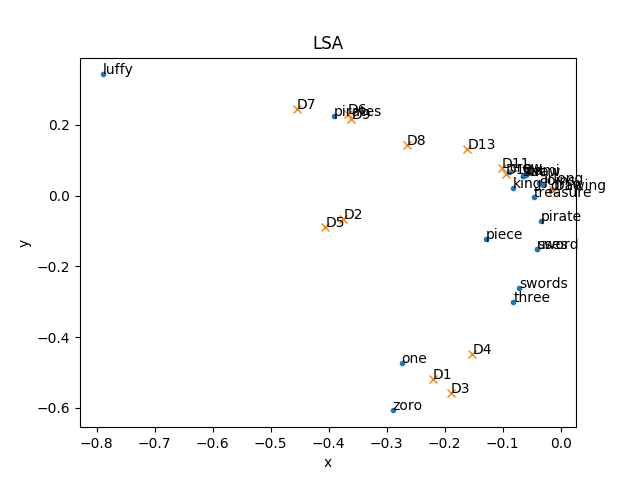
Inception

Inception结构

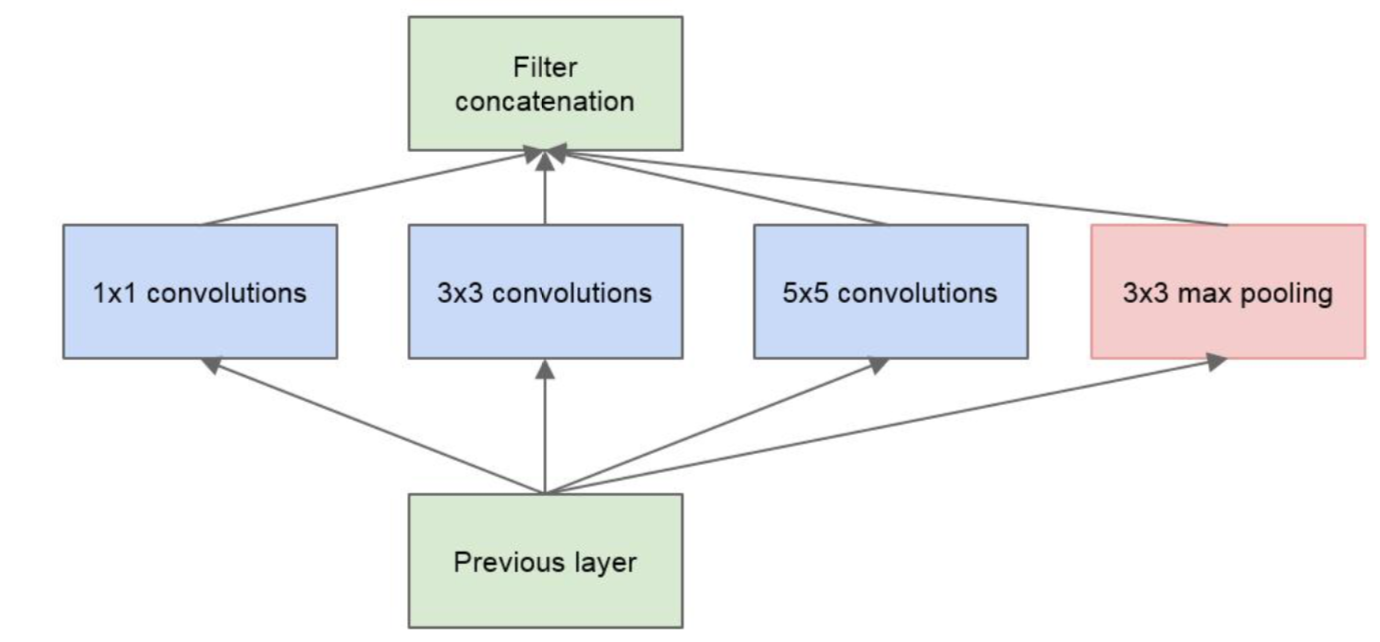
Inception架构的主要思想是找出如何让已有的稠密组件接近与覆盖卷积视觉网络中的最佳局部稀疏结构
为了避免patch校准问题, 现在滤波器大小限制在$1\ast1$, $3\ast3$和$5\ast5$, 主要为了方便, 不是必要的
另外在pooling层添加一个额外的并行pooling路径用于提高效率

Previous Layer, 输入层, 比如是$27\ast27\ast128$

先做一个$1\ast1$的卷积, 那么output为: $(27-1+1)/1=27, 27\ast27\ast?$
$3\ast3$的卷积, output为: $(27-3+1+2)/1=27, 27\ast27\ast?$
$5\ast5$的卷积, output为: $(27-5+1+4)/1=27, 27\ast27\ast?$
以上的三个卷积相当于从三个不同的方面并行的观察目标信息, 在这里比如$1\ast1$是10个, $3\ast3$是20个, $5\ast5$是5个, 那么输出到filter concatenation就是$27\ast27\ast35$, 就包含了小/中/大区域观测的结果

然而, 输入结果中有可能也包含着一些个性化的或者噪音数据或者异常信息, 所有要并行的做一个池化操作
池化的output为: (27-3+1+2)/1, 池化不改变深度, 所以是$27\ast27\ast128$

所以最后的层次为$27\ast27\ast(35+128)=27\ast27\ast163$

参数量为$(1\ast1\ast128+1)\ast10 + (3\ast3\ast128+1)\ast20 + (5\ast5\ast128+1)\ast5 = 40355$

这种结构参数比较多, 遂引出inception的改进结构

Inception结构改进/Pointwise Conv

架构的第二个主要思想: 在计算要求增加很多的地方应用维度缩减和预测. 即在$3\ast3$和$5\ast5$卷积前用一个$1\ast1$的卷积用于减少计算, 还用于修正线性激活. 如下图所示, 左边是加入维度缩减之前的, 右边是加入维度缩减之后的, 这就是Inception V1的网络架构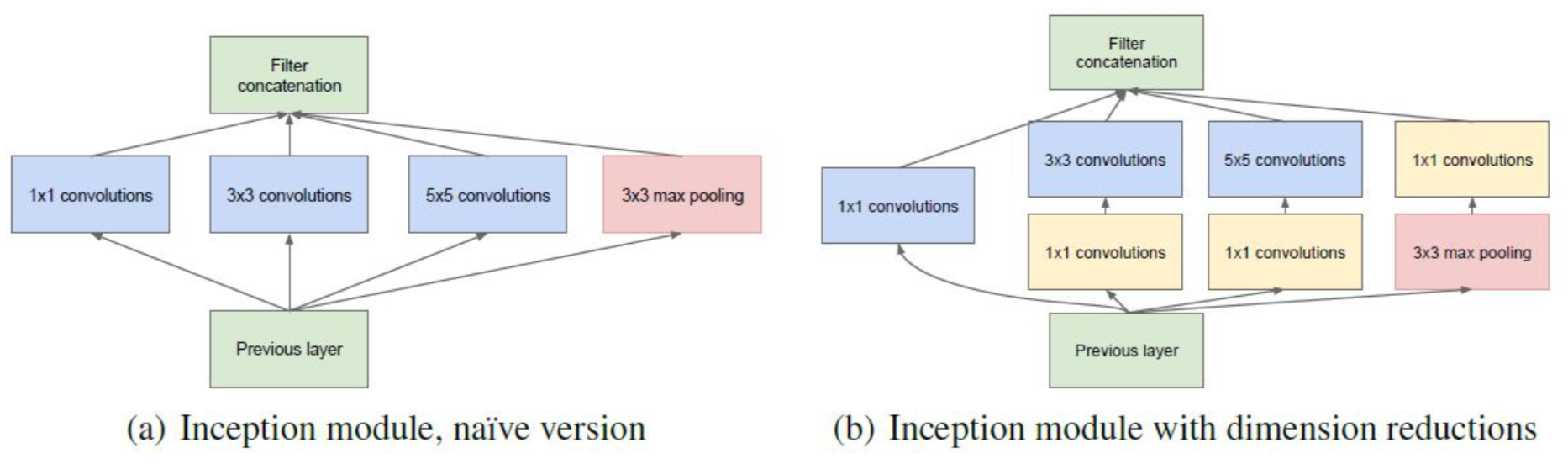

输入还是$27\ast27\ast128$, 假设核函数设置的都是10个

那么未改进的结构的总层数为$27\ast27\ast(10+10+10+128)=27\ast27\ast158$
参数量为$(1\ast1\ast128+1)\ast10 + (3\ast3\ast128+1)\ast10 + (5\ast5\ast128+1)\ast10 = 44830$
改进后的总层数为$27\ast27\ast40$
参数量为$(1\ast1\ast128+1)\ast10\ast4 + (3\ast3\ast10+1)\ast10 + (5\ast5\ast10+1)\ast10 = 8580$

改进后的结构就叫做Network-In-Network, 在上面的例子来说, 就是把128个方位的降为了40个方位

在这里$1 \ast 1$的卷积核就是Pointwise Convolution, 简称PW, 其目的主要在于减少维度, 还可以引入更多的非线性

Kernel Replace

Inception V2和Inception V3为了进一步降低卷积参数采用小卷积来代替大卷积

大尺寸的卷积核可以带来更大的感受野, 但也意味着会产生更多的参数, 比如$5 \ast 5$卷积核的参数有25个, $3 \ast 3$ 卷积核的参数有9个, 前者是后者的$\frac{25}{9}=2.78$倍. 因此, GoogLeNet团队提出可以用2个连续的$3 \ast 3$卷积层组成的小网络来代替单个的$5 \ast 5$卷积层, 即在保持感受野范围的同时又减少了参数量. 除了规整的的正方形, 还有分解版本的$3 \ast 3 = 3 \ast 1 + 1 \ast 3$，这个效果在深度较深的情况下比规整的卷积核更好(feature map大小建议在12到20之间)

Group Conv/Depthwise Separable Conv

Group COnv

Group Conv分组卷积, 可以用来切分网络, 以便在多个GPU上运行

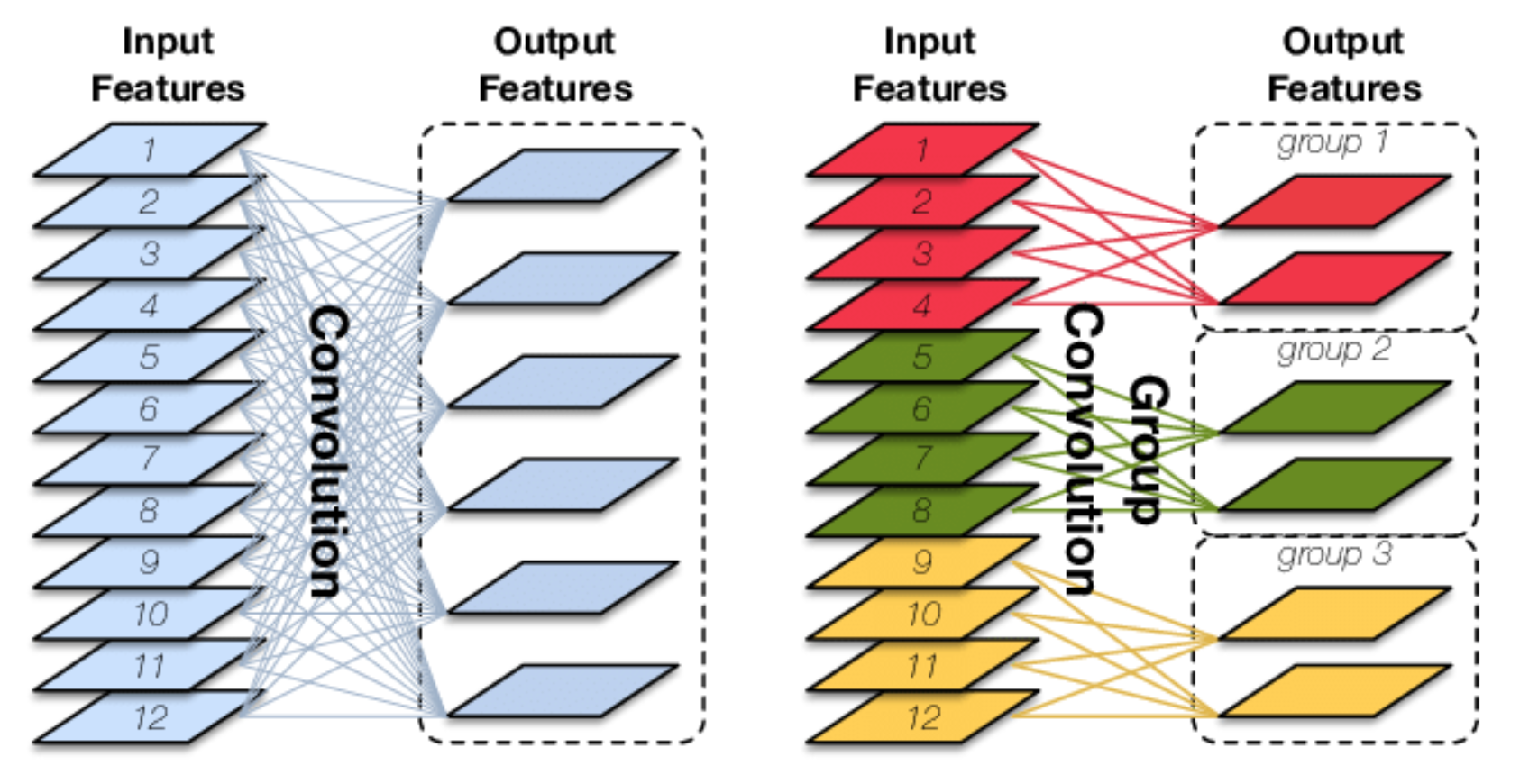
对于输入为$I \ast H \ast W$大小的input features, 经过O个$K \ast K \ast I$大小的卷积核之后, 输出的output features通道数为O, 卷积参数量为$O \ast K \ast K \ast I$

Group Conv, 先对输入的input features进行分组, 然后对每组分别进行卷积. 仍然假设input feature map的尺寸为$I \ast H \ast W$, 输出output features的通道数为O, 假设分成G个组, 则每个input feature map的数量为$\frac{I}{G}$, 每组的输出的feature map的数量为$\frac{O}{G}$, 那么每个卷积核的尺寸为$K \ast K \ast \frac{I}{G}$, 每组卷积核的数量为$\frac{O}{G}$, 卷积核的总数仍然为O.

卷积核只与自己同组的input feature map进行卷积, 最后的卷积的总参数量为$O \ast K \ast K \ast \frac{I}{G}$, 由此可以看到总参数量减少到了原来的$\frac{1}{G}$

Group Conv的用途如下所示:

• 减少参数量, 分成G组, 则参数量减少为原来的$\frac{1}{G}$
• Group Conv可以看成是一种structured sparse, 每个卷积核的尺寸由$K \ast K \ast I$变成了$K \ast K \ast \frac{I}{G}$, 那么减少的参数量为$(I - \frac{I}{G})$, 可以视其为0(考虑该效果是否与L1/L2正则类似)

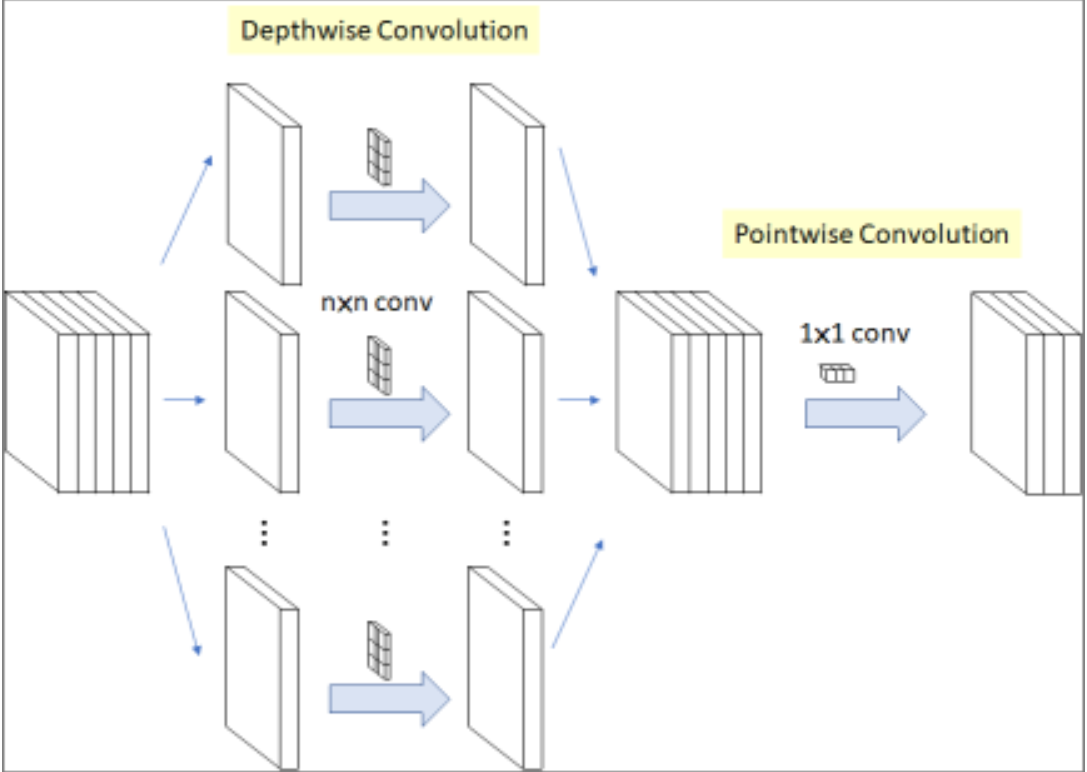
Depthwise Convolution(DW)是Group Conv的一种特例. 当分组数量等于input feature map的数量, output feature map数量也等于input feature map数量, 即当$I = O = G$, 且O个卷积核中每个的尺寸为$K \ast K \ast 1$时, Group Conv 就成了Depthwise Conv.

Depthwise Separable Conv

Depthwise Separable Convolution则是DW + PW的组合, 参数量会进一步缩小, 如下图所示:

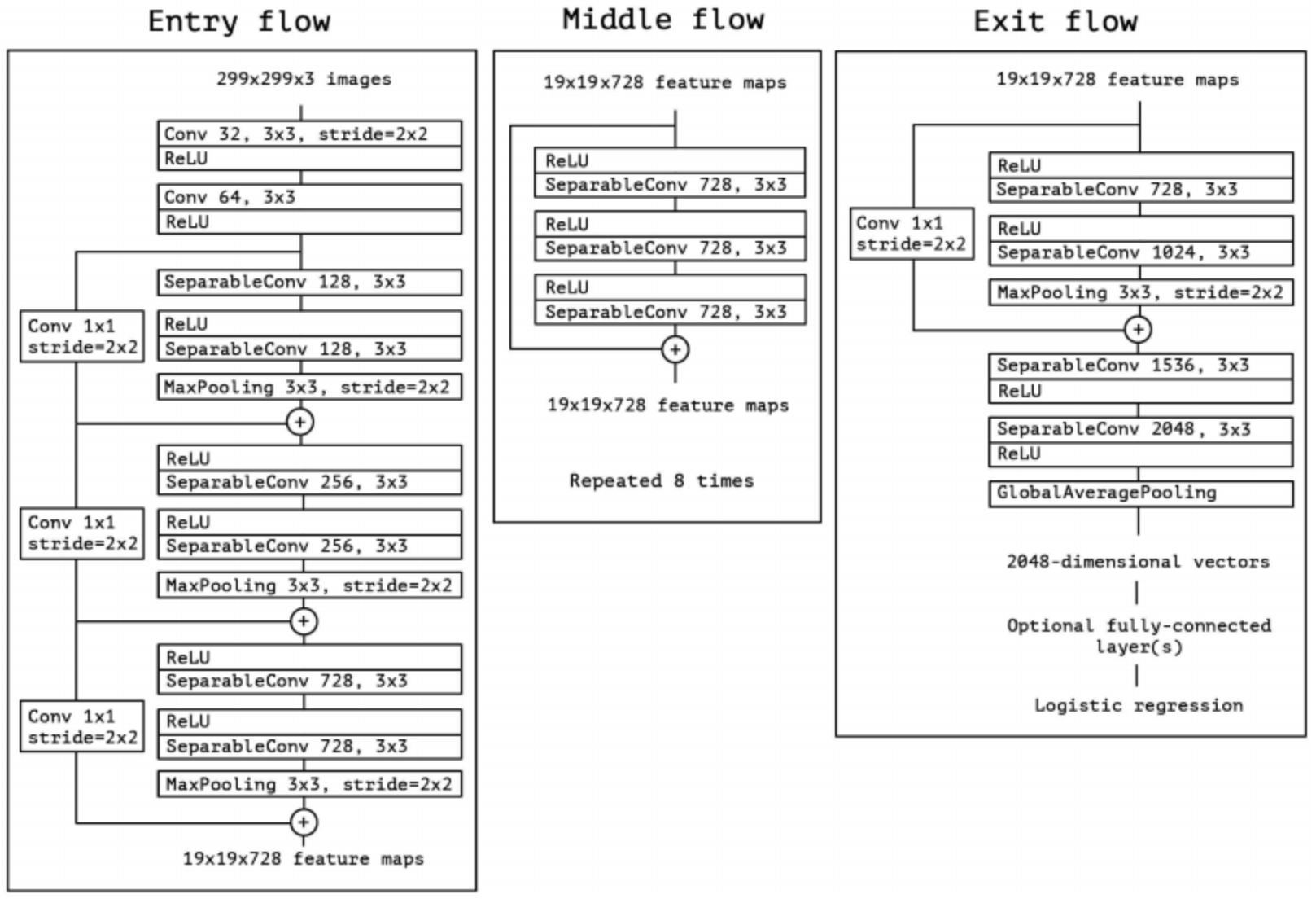
Xception

Xception就是在Inception + Depthwise Separable Conv

Inception Hypothesis

从Inception的各种演进架构可以看出, Inception V1是从多尺寸卷积核角度来观察input feature map, Inception V3是从参数量和计算量角度来尝试改进结构的.

然而Inception V3也可以理解为: 通过显式地将操作分解为一系列独立的通道维度和空间维度的学习, 从而使得学习的过程更加简单和高效.

Inception V1里各个卷积核需要同时学习空间上的相关性和通道相关性, 结合了spatial dimentions和channels dimentions.

Inception V3先通过一组$1 \ast 1$PW卷积来学习通道相关性, 将输入数据映射到多个单独的小空间(降维), 之后对所有这些小空间, 通过常规的$3 \ast 3$卷积和$5 \ast 5$卷积来学习空间相关性.

Inception背后的基本假设是, 通道相关性和空间相关性是可以分离相互之间的耦合性的, 于是就得到了Xception: 将通道相关性和空间相关性分开学习的结构.

Extreme Inception

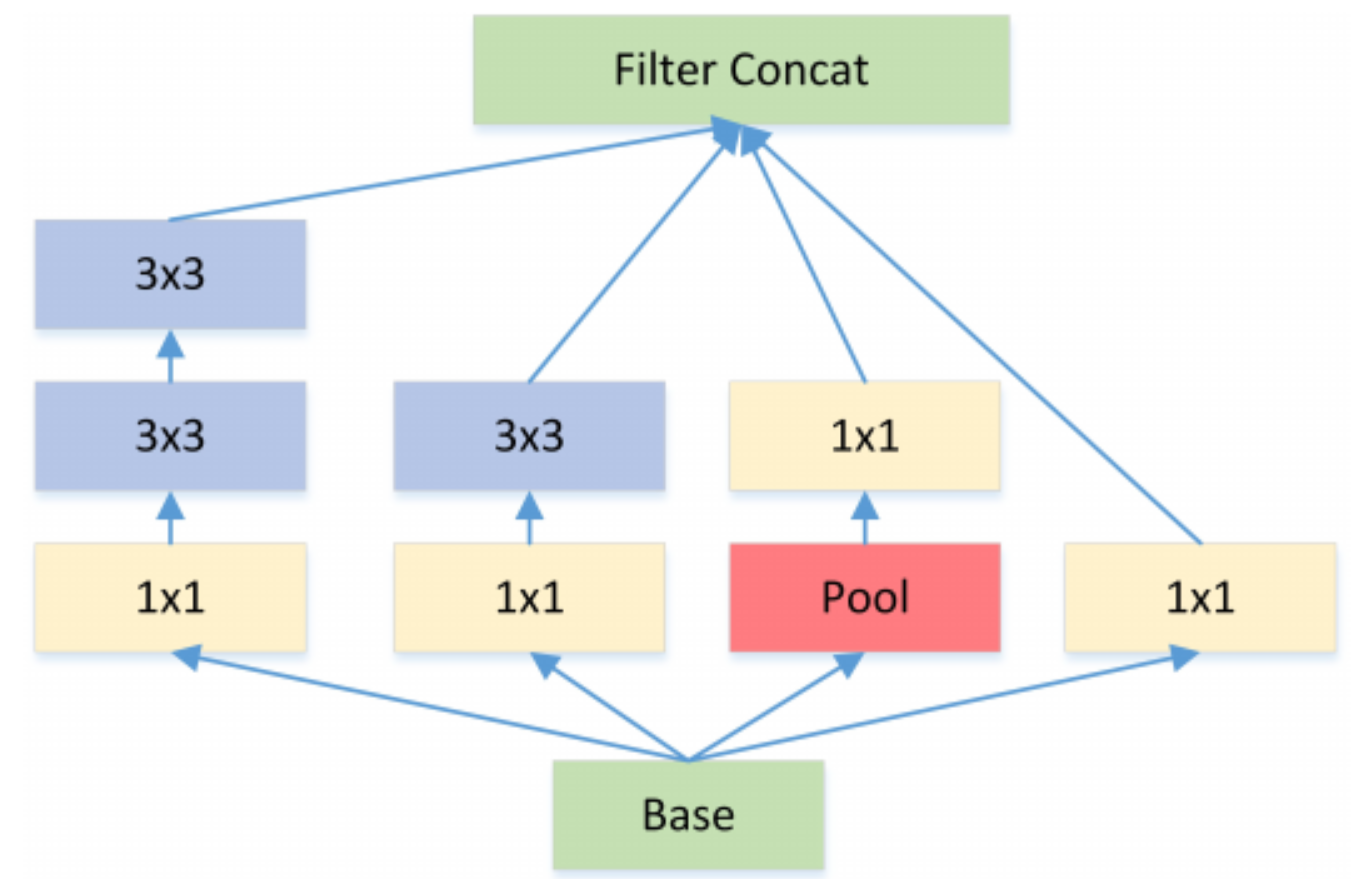
Inception中, 特征是通过$1 \ast 1$, $3 \ast 3$, $5 \ast 5$, max pooling等进行提取的, Inception结构将特征类型的选择留给网络自己训练, 即同一个输入交由几种特征提取方式, 之后做concat. Inception V3结果图如下:

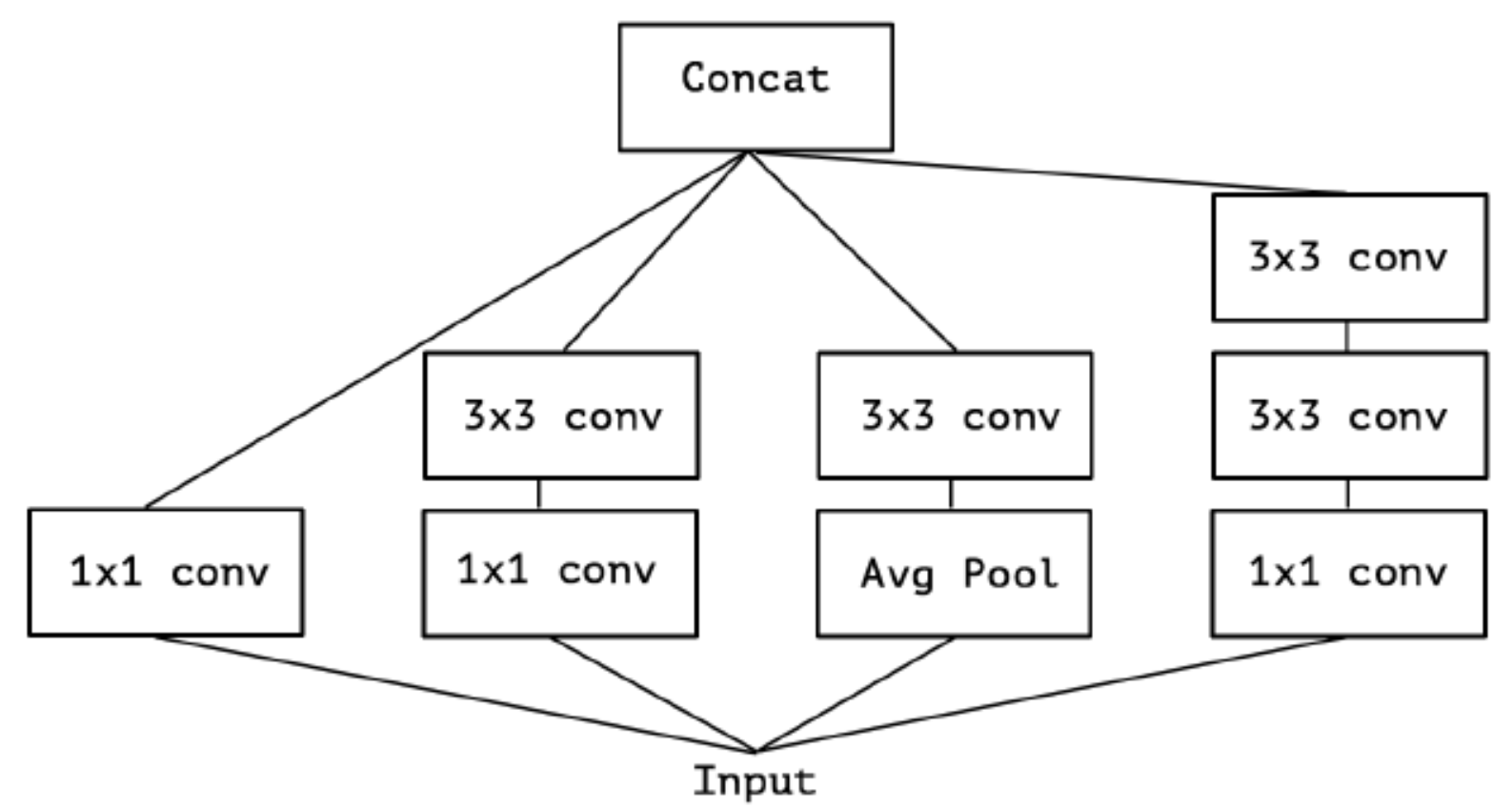
对Inception-V3进行简化, 去除Inception-V3中的avg-pooling, 输入的下一步操作就都是$1 \ast 1$的PW卷积了:

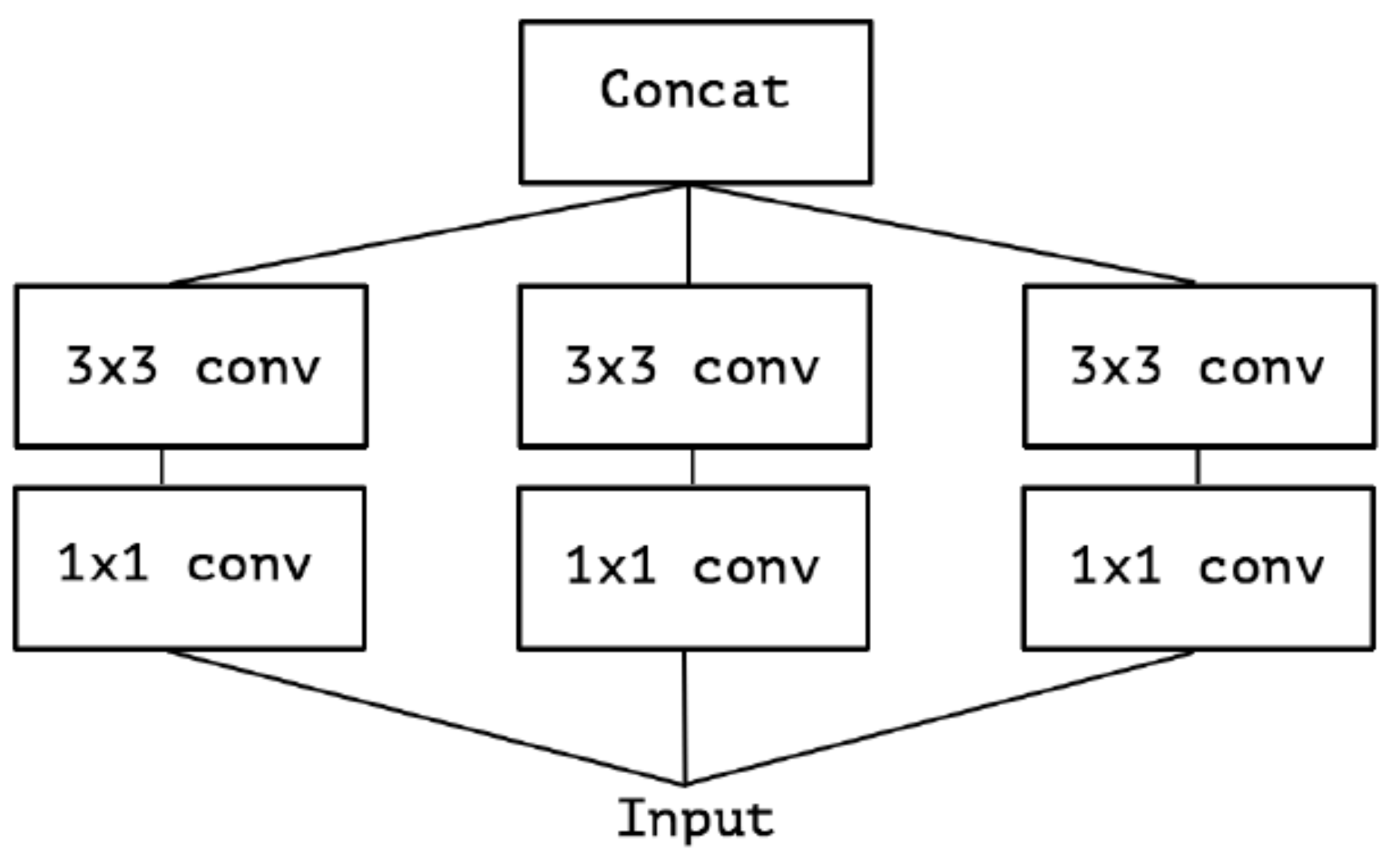
继续演进, 3个PW卷积核统一起来变成共用一个PW卷积, 后面的三个$3 \ast 3$卷积核则分别负责Group Conv

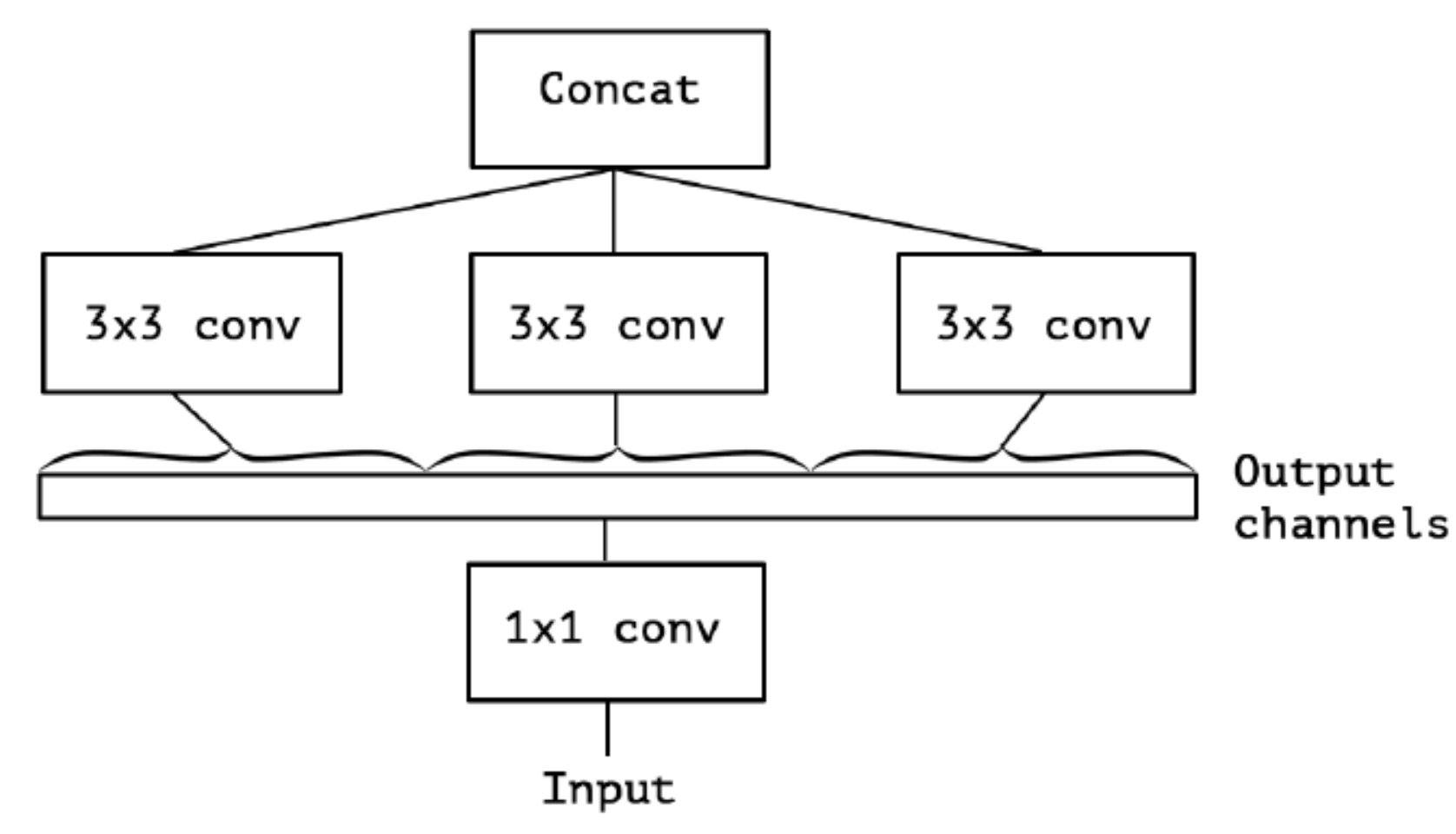
对卷积后的每个channel分别进行$3 \ast 3$卷积操作(Depthwise Conv, DW), 最后concat, 就是Extreme Inception:

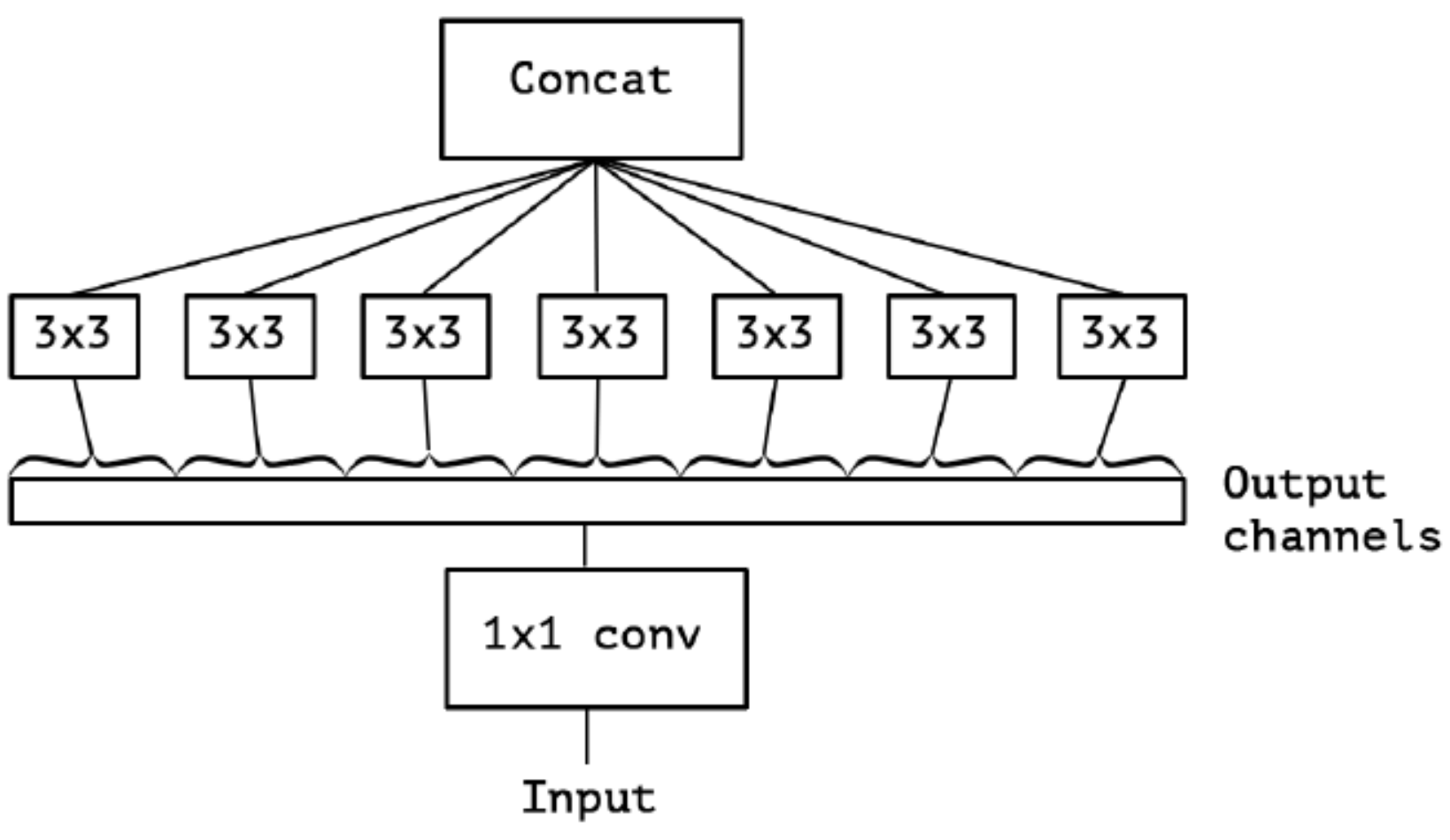
在Extreme Inception模块中, 用于学习空间相关性的$3 \ast 3$的DW卷积, 和用于学习通道相关性的$1 \ast 1$PW卷积之间, 不使用非线性激活函数, 收敛过程更快, 准确率更高.

Xception

Xception常用版本是将DW和PW互换位置.

Extreme Inception先进行$1 \ast 1$的PW卷积, 再进行$3 \ast 3$的DW卷积.
Depthwise Seprable Conv先进行$3 \ast 3$的DW卷积, 再进行$1 \ast 1$的PW卷积.

DW与标准卷积操作的计算量比较如下:

其中I为输入通道数, O为输出通道数, K为标准卷积和大小. 当使用$3 \ast 3$的卷积核时, 参数量约等于标准卷积核的$\frac{1}{9}$, 大大的减少了参数量, 从而加快了训练速度. 最终其网络结构图如下图所示:

参考

深度学习笔记
深度学习背景下的神经网络架构演变

如何用极大似然概率解释交叉熵loss

Logistic回归

Logistic/Sigmoid函数, $\displaystyle p = h_\theta(x) = g(\theta^Tx) = \frac{1}{1 + e^{-\theta^Tx}}$, p是个概率值

Logistic回归及似然函数

假设:

似然函数:

最大似然/极大似然函数的随机梯度
对数似然函数为:

极大似然估计与Logistic回归损失函数

如果我们对m个样本取平均, 得到如下:

即cross entropy

详情参考

硬币问题为何不使用MLP而直接假设正反面概率p?

1. 对于硬币游戏, 硬币只有正面和反面两种情况, 那么对于同一个硬币来说, 正面的概率是$p$的话, 那么反面的概率就是$1-p$, 根据一个已知的硬币观测序列, 可以直接将观测到的正反面情况带入相应的概率公式, 通过梯度下降得到极值;
2. 而MLP分为输入层, 隐藏层, 输出层, 层级之间使用全连接, 需要将特征值传入进去, 通过带有结果的数据来训练神经网络的weight和bias, 本质上是将线性不可分的数据通过增加隐藏层构造切分平面使之线性科锋, 解决的问题基本上是分类问题.

面对未知分类问题，存在A,B,C三个模型，如何确定使用哪一个模型？

• 模型选择, 对特定任务最优建模方法的选择或者对特定模型最佳参数的选择
• 在训练数据集上运行模型(算法)并在测试数据集中测试效果, 迭代进行数据模型对修改, 这种方式称为交叉验证(将原始数据分为训练集和测试集, 使用训练集构建模型, 并使用测试集评估模型提供修改意见)
• 模型的选择会尽可能多的选择算法进行执行, 并比较执行结果
• 模型的测试一般从以下几个方面来进行比较, 分别是准确率, 召回率, 精准率, F值
  • 准确率(Accuracy) = 提取出的正确样本数/总样本数
  • 召回率(Recall) = 正确的正例样本数/样本中的正例样本数- 覆盖率
  • 精确度(Precision) = 正确的正例样本数/预测为正例的样本数
  • F值 = Precision Recall 2 / (Precision + Recall), 即F值是精准度和召回率的调和平均值

true positive(hit)真正例, 确实是正例
true negative(Correct Rejection)真负例, 确实是负例
false positive(False Alarm)假正例, 本来真实值是负例, 被预测为正例了, 虚报, 干扰报警
false negative(Miss)假负例, 本来真实值是正例, 被预测为负例了, 即没有预测出来

击中(Hit)(报准)和正确拒绝(Correct Rejection)是正确反应, 虚报(False Alarm)和漏报(Miss)是错误反应

A和D预测正确, B和C预测错误, 那么计算结果为:

举个例子, 真实值中, 正例为80, 负例为20; 预测值中, 正例为90, 负例为10, 然而, 在模型的实际预测中, 原本有75个真正的正例, 有15个是假正例, 5个假负例和5个真负例, 如下图所示:

Accuracy和Recall是一对互斥的关系, Accuracy在增大的时候Recall是在减小的

ROC

ROC(Receiver Operating Characteristic), 描述的是分类混淆矩阵中FPR-TPR之间的相对变化情况.
纵轴是TPR(True Positive Rate), 横轴是FPR(False Positive Rate)

如果二元分类器输出的是对正样本对一个分类概率值, 当取不同阈值时会得到不同当混淆矩阵， 对应于ROC曲线上当一个点, ROC曲线就反应了FPR和TPR之间权衡当情况, 通俗的说, 即在TPR随着FPR递增的情况下, 谁增长的更快, 快多少的问题. TPR增长的越快, 曲线越往上弯曲, AUC就越大, 反应了模型的分类性能就越好. 当正负样本不平衡时, 这种模型评价方式比起一般当精确度评价方式的好处尤其显著.

AUC(Area Under Curve)

AUC被定义为ROC曲线下的面积, 显然这个面积的数值不会大于1. 由于ROC曲线一般都处于y=x这条直线的上方, 所以AUC的取之范围在0.5和1之间. AUC作为数值可以直观的评价分类器的好坏, 值越大越好.

AUC的值一般要求在0.7以上.

模型评估

回归结果度量

• explained_varicance_score, 可解释方差的回归评分函数
• mean_absolute_error, 平均绝对误差
• mean_squared_error, 平均平方误差

模型评估总结_分类算法评估方式

思考题

在scope例子中加入tensorboard, 并观察可视化图与没有scope的变化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

import tensorflow as tf

with tf.device('/cpu:0'):
    with tf.variable_scope('foo'):
        x_init1 = tf.get_variable('init_x', [10], dtype=tf.float32, initializer=tf.random_normal_initializer())[0]
        x = tf.Variable(initial_value=x_init1, name='x')
        y = tf.placeholder(dtype=tf.float32, name='y')
        z = x + y

    with tf.variable_scope('bar'):
        a = tf.constant(3.0) + 4.0

    w = z * a

# 开始利用tf.summary记录图的信息, 需要展示的信息

tf.summary.scalar('scalar_x_init1', x_init1)
tf.summary.scalar(name='scalar_x', tensor=x)
tf.summary.scalar(name='scalar_y', tensor=y)
tf.summary.scalar(name='scalar_z', tensor=z)
tf.summary.scalar(name='scalar_w', tensor=w)

# update操作, 这里只能更新x
assign_op = tf.assign(x, x + 1)

with tf.control_dependencies([assign_op]):
    with tf.device('/gpu:0'):
        out = x * y
        tf.summary.scalar(name='scalar_out', tensor=out)

with tf.Session(config=tf.ConfigProto(allow_soft_placement=True, log_device_placement=True)) as sess:
    # merge所有的summary, 触发所有的输出操作
    merged_summary = tf.summary.merge_all()
    # 得到文件的输出对象
    writer = tf.summary.FileWriter('./result', sess.graph)
    # 初始化
    sess.run(tf.global_variables_initializer())
    # print

    for i in range(1, 5):
        summary, r_out, r_x, r_w = sess.run([merged_summary, out, x, w], feed_dict={y: i})
        writer.add_summary(summary, i)
        print("{}, {}, {}".format(r_out, r_x, r_w))

1

tensorboard --logdir tensorflow_excise/result

MNIST DNN中single-layer.py和single-layer-optimization.py的结果是有差距, 寻找原因

编程题

MNIST DNN例子中实现cross entropy;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

# by cangye@hotmail.com
# 引入库
from tensorflow.examples.tutorials.mnist import input_data
import tensorflow as tf

# 获取数据
mnist = input_data.read_data_sets("../data/", one_hot=True)
# 定义全链接层函数
def full_layer(input_tensor, out_dim, name='full'):
    with tf.variable_scope(name):
        shape = input_tensor.get_shape().as_list()
        W = tf.get_variable('W', (shape[1], out_dim), dtype=tf.float32,
                            initializer=tf.truncated_normal_initializer(stddev=0.1))
        b = tf.get_variable('b', [out_dim], dtype=tf.float32, initializer=tf.constant_initializer(0))
        out = tf.matmul(input_tensor, W) + b
    return tf.nn.sigmoid(out)


def model(net, out_dim):
    net = full_layer(net, out_dim, "full_layer1")
    return net


# 定义输入
with tf.variable_scope("inputs"):
    x = tf.placeholder(tf.float32, [None, 784])
    label = tf.placeholder(tf.float32, [None, 10])
# 引入模型
y = model(x, 10)
# 定义损失函数
# loss = tf.reduce_mean(tf.square(y - label))
ce = tf.nn.softmax_cross_entropy_with_logits(labels=label, logits=y)
loss = tf.reduce_mean(ce)
# 用梯度迭代算法
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)
# 用于验证
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(label, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# 定义会话
sess = tf.Session()
# 初始化所有变量
sess.run(tf.global_variables_initializer())
# 迭代过程
train_writer = tf.summary.FileWriter("mnist-logdir", sess.graph)
for itr in range(10000):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    sess.run(train_step, feed_dict={x: batch_xs, label: batch_ys})
    if itr % 10 == 0:
        print("step:%6d  accuracy:" % itr, sess.run(accuracy, feed_dict={x: mnist.test.images,
                                                                         label: mnist.test.labels}))

# 这下面的部分用于绘图
import matplotlib.pyplot as plt
import numpy as np
import matplotlib as mpl

mpl.style.use('fivethirtyeight')
# 获取W取值
with tf.variable_scope("full_layer1", reuse=True):
    W = tf.get_variable("W")
W = sess.run(W.value())
# 绘图过程
fig = plt.figure()
ax = fig.add_subplot(221)
ax.matshow(np.reshape(W[:, 1], [28, 28]), cmap=plt.get_cmap("Purples"))
ax = fig.add_subplot(222)
ax.matshow(np.reshape(W[:, 2], [28, 28]), cmap=plt.get_cmap("Purples"))
ax = fig.add_subplot(223)
ax.matshow(np.reshape(W[:, 3], [28, 28]), cmap=plt.get_cmap("Purples"))
ax = fig.add_subplot(224)
ax.matshow(np.reshape(W[:, 4], [28, 28]), cmap=plt.get_cmap("Purples"))
plt.show()

在IRIS例子中实现cross entropy代替MSE和sigmoid

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

# by cangye@hotmail.com
# TensorFlow入门实例

import pandas as pd
import tensorflow as tf
import tensorflow.contrib.slim as slim
import numpy as np


def variable_summaries(var, name="layer"):
    with tf.variable_scope(name):
        mean = tf.reduce_mean(var)
        tf.summary.scalar('mean', mean)
        with tf.name_scope('stddev'):
            stddev = tf.sqrt(tf.reduce_mean(tf.square(var - mean)))
        tf.summary.scalar('stddev', stddev)
        tf.summary.scalar('max', tf.reduce_max(var))
        tf.summary.scalar('min', tf.reduce_min(var))
        tf.summary.histogram('histogram', var)


data = pd.read_csv("../data/iris.data.csv")
c_name = set(data.name.values)
print(c_name)
iris_label = np.zeros([len(data.name.values), len(c_name)])
iris_data = data.values[:, :-1]
iris_data = iris_data - np.mean(iris_data, axis=0)
iris_data = iris_data / np.max(iris_data, axis=0)
train_data = []
train_data_label = []
test_data = []
test_data_label = []
for idx, itr_name in enumerate(c_name):
    datas_t = iris_data[data.name.values == itr_name, :]
    labels_t = np.zeros([len(datas_t), len(c_name)])
    labels_t[:, idx] = 1
    train_data.append(datas_t[:30])
    train_data_label.append(labels_t[:30])
    test_data.append(datas_t[30:])
    test_data_label.append(labels_t[30:])
train_data = np.concatenate(train_data)
train_data_label = np.concatenate(train_data_label)
test_data = np.concatenate(test_data)
test_data_label = np.concatenate(test_data_label)
x = tf.placeholder(tf.float32, [None, 4], name="input_x")
label = tf.placeholder(tf.float32, [None, 3], name="input_y")
# 对于sigmoid激活函数而言，效果可能并不理想
net = slim.fully_connected(x, 4, activation_fn=tf.nn.relu, scope='full1', reuse=False)
net = tf.contrib.layers.batch_norm(net)
net = slim.fully_connected(net, 8, activation_fn=tf.nn.relu, scope='full2', reuse=False)
net = tf.contrib.layers.batch_norm(net)
net = slim.fully_connected(net, 8, activation_fn=tf.nn.relu, scope='full3', reuse=False)
net = tf.contrib.layers.batch_norm(net)
net = slim.fully_connected(net, 4, activation_fn=tf.nn.relu, scope='full4', reuse=False)
net = tf.contrib.layers.batch_norm(net)
y = slim.fully_connected(net, 3, activation_fn=tf.nn.sigmoid, scope='full5', reuse=False)

ce = tf.nn.softmax_cross_entropy_with_logits(labels=label, logits=y)
loss = tf.reduce_mean(ce)
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(label, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

# train_step = tf.train.GradientDescentOptimizer(0.5).minimize(loss)
optimizer = tf.train.GradientDescentOptimizer(0.5)
var_list_w = [var for var in tf.trainable_variables() if "w" in var.name]
var_list_b = [var for var in tf.trainable_variables() if "b" in var.name]
gradient_w = optimizer.compute_gradients(loss, var_list=var_list_w)
gradient_b = optimizer.compute_gradients(loss, var_list=var_list_b)
for idx, itr_g in enumerate(gradient_w):
    variable_summaries(itr_g[0], "layer%d-w-grad" % idx)
for idx, itr_g in enumerate(gradient_b):
    variable_summaries(itr_g[0], "layer%d-b-grad" % idx)
for idx, itr_g in enumerate(var_list_w):
    variable_summaries(itr_g, "layer%d-w" % idx)
for idx, itr_g in enumerate(var_list_b):
    variable_summaries(itr_g, "layer%d-b" % idx)
train_step = optimizer.apply_gradients(gradient_w + gradient_b)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
train_writer = tf.summary.FileWriter("logdir-bn", sess.graph)
merged = tf.summary.merge_all()
for itr in range(600):
    sess.run(train_step, feed_dict={x: train_data, label: train_data_label})
    if itr % 30 == 0:
        acc1 = sess.run(accuracy, feed_dict={x: train_data, label: train_data_label})
        acc2 = sess.run(accuracy, feed_dict={x: test_data, label: test_data_label})
        print("step:{:6d}  train:{:.3f} test:{:.3f}".format(itr, acc1, acc2))
        summary = sess.run(merged, feed_dict={x: train_data, label: train_data_label})
        train_writer.add_summary(summary, itr)

思考: 硬币

硬币a和硬币b, 抛硬币a朝上的概率为0.7, 抛硬币b朝上的概率为0.4

问题1: 从一个黑盒中随机取出一个, 向上抛10次, 结果有6次朝上, 那么拿的是哪个硬币, 为什么?
问题2: 分别来自a和b的概率是多少?
问题3: 向上抛20次, 有12次正面朝上的概率是多少?

分析

设向上抛硬币a和b是事件A, 那么,
抛硬币a朝上的概率为0.7, 记为$P(A_1) = 0.7$, 抛硬币b朝上的概率为0.4, 记为$P(A_2) = 0.4$
向上抛10次结果有6次朝上为事件B, 记为$P(B)$

或者

向上抛20次, 12次正面朝上的概率为:

思考: 为什么SVD之后cos距离最近

几何中夹角余弦可用来衡量两个向量方向的差异, 所以可以用余弦相似度来衡量样本向量之间的差异
所以在文本做完SVD之后, 用余弦相似度来衡量输入文本中每个文档(即每句话)之间的相似度

编程: 病情预测

6位建筑工人历史病例数据如下:

根据以上历史数据, 预测新来的一位打喷嚏的建筑工人患感冒的概率

分析

从上述数据, 可以直观的得到, 症状列表为$[“打喷嚏”, “头痛”]$, 职业列表为$[“护士”, “建筑工人”, “教师”, “农夫”]$, 疾病列表为$[“感冒”, “过敏”, “脑震荡”]$

统计

如果从2种症状判断为3种疾病的关系表如下:

统计如下:

或者如下(将行列转置一下):

如果从4种职业判断为3种疾病的关系表如下:

或者如下(将行列转置一下):

从T1(症状-疾病表), 得到:

P(感冒|打喷嚏) = 2/3, P(打喷嚏|感冒) = 2/3
P(感冒|头痛) = 1/3, P(头痛|感冒) = 1/3

P(过敏|打喷嚏) = 1, P(打喷嚏|过敏) = 1/1
P(过敏|头痛) = 0, P(头痛|过敏) = 0/1

P(脑震荡|打喷嚏) = 0, P(打喷嚏|脑震荡) = 0/2
P(脑震荡|头痛) = 1, P(头痛|脑震荡) = 2/2

P(打喷嚏) = 3/6
P(头痛) = 3/6

P(感冒) = 3/6
P(过敏) = 1/6
P(脑震荡) = 2/6

从T2(职业-疾病表), 得到:

P(感冒|护士) = 1/1, P(护士|感冒) = 1/3
P(过敏|护士) = 0/1, P(护士|过敏) = 0/1
P(脑震荡|护士) = 0/1, P(护士|脑震荡) = 0/2

P(感冒|农夫) = 0/1, P(农夫|感冒) = 0/3
P(过敏|农夫) = 1/1, P(农夫|过敏) = 1/1
P(脑震荡|农夫) = 0/1, P(农夫|脑震荡) = 0/2

P(感冒|建筑工人) = 1/2, P(建筑工人|感冒) = 1/3
P(过敏|建筑工人) = 0/2, P(建筑工人|过敏) = 0/1
P(脑震荡|建筑工人) = 1/2, P(建筑工人|脑震荡) = 1/2

P(感冒|教师) = 1/2, P(教师|感冒) = 1/3
P(过敏|教师) = 0/2, P(教师|过敏) = 0/1
P(脑震荡|教师) = 1/2, P(教师|脑震荡) = 1/2

P(护士) = 1/6
P(农夫) = 1/6
P(建筑工人) = 2/6
P(教师) = 2/6

P(感冒) = 3/6
P(过敏) = 1/6
P(脑震荡) = 2/6

计算结果

编程实现

history.csv

1
2
3
4
5
6
7

症状,职业,疾病
打喷嚏,护士,感冒
打喷嚏,农夫,过敏
头痛,建筑工人,脑震荡
头痛,建筑工人,感冒
打喷嚏,教师,感冒
头痛,教师,脑震荡

predict_sick.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88

import numpy as np
import pandas as pd

"""
症状列表:
[“打喷嚏”,“头痛”]
职业列表:
[“护士”,“建筑工人”,“教师”,“农夫”]
疾病列表:
[“感冒”,“过敏”,“脑震荡”]
历史数据:
症状, 职业, 疾病
打喷嚏, 护士, 感冒
打喷嚏, 农夫, 过敏
头痛, 建筑工人, 脑震荡
头痛, 建筑工人, 感冒
打喷嚏, 教师, 感冒
头痛, 教师, 脑震荡
"""

data = pd.read_csv('history.csv')
print(data)

sickness = data["疾病"].value_counts()
occupation = data["职业"].value_counts()
symptom = data["症状"].value_counts()
print(sickness)
print(occupation)
print(symptom)

# P(打喷嚏)
p_pengti = symptom["打喷嚏"] / sum(symptom)
print(f"p_pengti:\n {p_pengti}")

# P(建筑工人)
p_worker = occupation["建筑工人"] / sum(occupation)
print(f"p_worker:\n {p_worker}")

# P(感冒)
p_cold = sickness["感冒"] / sum(sickness)
print(f"p_cold:\n {p_cold}")

# P(建筑工人|感冒)
df_worker_cold = data[["职业", "疾病"]]
print(f"df_worker_cold:\n {df_worker_cold}")
for index, row in df_worker_cold.iterrows():
    if row["疾病"] == "感冒":
        df_worker_cold["疾病"][index] = 1
        if row["职业"] == "建筑工人":
            df_worker_cold["职业"][index] = 1
        else:
            df_worker_cold["职业"][index] = 0
    else:
        df_worker_cold["疾病"][index] = 0
        if row["职业"] == "建筑工人":
            df_worker_cold["职业"][index] = 1
        else:
            df_worker_cold["职业"][index] = 0

print(f"df_worker_cold:\n {df_worker_cold}")
p_worker_cold = (df_worker_cold["职业"] & df_worker_cold["疾病"]).sum() / df_worker_cold["疾病"].sum()
print(f"p_worker_cold:\n {p_worker_cold}")

# P(打喷嚏|感冒)
df_pengti_cold = data[["症状", "疾病"]]
print(f"df_pengti_cold:\n {df_pengti_cold}")
for i, j in df_pengti_cold.iterrows():
    # print(i, j)
    if j["疾病"].strip() == "感冒":
        df_pengti_cold["疾病"][i] = 1
        if j["症状"] == "打喷嚏":
            df_pengti_cold["症状"][i] = 1
        else:
            df_pengti_cold["症状"][i] = 0
    else:
        df_pengti_cold["疾病"][i] = 0
        if j["症状"] == "打喷嚏":
            df_pengti_cold["症状"][i] = 1
        else:
            df_pengti_cold["症状"][i] = 0

print(f"df_pengti_cold:\n {df_pengti_cold}")
p_pengti_cold = (df_pengti_cold["症状"] & df_pengti_cold["疾病"]).sum() / df_pengti_cold["疾病"].sum()
print(f"p_pengti_cold:\n {p_pengti_cold}")

# P(感冒|建筑工人,打喷嚏)
p_cold_worker_and_pengti = (p_worker_cold * p_pengti_cold * p_cold) / (p_worker * p_pengti)
print(f"p_cold_worker_and_pengti:\n {p_cold_worker_and_pengti}")

编程: 在SVD基础上进行TF-IDF

• 将一个文本当作一个无序的数据集合, 文本特征可以采用文本中的词条T进行体现, 那么文本中出现的所有词条及其出现的次数就可以体现文档的特征
• TF-IDF, 词条的重要性随着它在文件中出现的次数成正比增加, 但同时会随着它在语料库中出现的频率成反比下降;
  • 词条在文本中出现的次数越多, 表示该词条对该文本的重要性越高
  • 词条在所有文本中出现的次数越少, 说明这个词条对文本的重要性越高
  • TF(词频)指某个词条在文本中出现的次数, 一般会将其进行归一化处理(该词条数量/该文档中所有词条数量)
  • IDF(逆向文件频率)指一条词条重要性的度量, 一般计算方式为总文件数目除以包含该词语之文件的数目, 再将得到的商取对数得到. TF-IDF即TF*IDF

注意: IDF取对数时，分母$+1$是为了方式分母为0

tf-idf-svd.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146

import numpy as np
import pylab
import re
from scipy import linalg
from matplotlib import pyplot

# 文档
documents = [
    "Roronoa Zoro, nicknamed \"Pirate Hunter\" Zoro, is a fictional character in the One Piece franchise created by Eiichiro Oda.",
    "In the story, Zoro is the first to join Monkey D. Luffy after he is saved from being executed at the Marine Base. ",
    "Zoro is an expert swordsman who uses three swords for his Three Sword Style, but is also capable of the one and two-sword styles. ",
    "Zoro seems to be more comfortable and powerful using three swords, but he also uses one sword or two swords against weaker enemies.",
    "In One Piece, Luffy sails from the East Blue to the Grand Line in search of the legendary treasure One Piece to succeed Gol D. Roger as the King of the Pirates. ",
    "Luffy is the captain of the Straw Hat Pirates and along his journey, he recruits new crew members with unique abilities and personalities. ",
    "Luffy often thinks with his stomach and gorges himself to comical levels. ",
    "However, Luffy is not as naive as many people believe him to be, showing more understanding in situations than people often expect. ",
    "Knowing the dangers ahead, Luffy is willing to risk his life to reach his goal to become the King of the Pirates, and protect his crew.",
    "Adopted and raised by Navy seaman turned tangerine farmer Bellemere, Nami and her older sister Nojiko, have to witness their mother being murdered by the infamous Arlong.",
    "Nami, still a child but already an accomplished cartographer who dreams of drawing a complete map of the world, joins the pirates, hoping to eventually buy freedom for her village. ",
    "Growing up as a pirate-hating pirate, drawing maps for Arlong and stealing treasure from other pirates, Nami becomes an excellent burglar, pickpocket and navigator with an exceptional ability to forecast weather.",
    "After Arlong betrays her, and he and his gang are defeated by the Straw Hat Pirates, Nami joins the latter in pursuit of her dream."
]

print(f'len(documents): {len(documents)}')
# 停用词
stopwords = ['a', 'an', 'after', 'also', 'and', 'as', 'be', 'being', 'but', 'by', 'd', 'for', 'from', 'he', 'her',
             'his', 'in', 'is', 'more', 'of', 'often', 'the', 'to', 'who', 'with', 'people']
# 要去除的标点符号的正则表达式
punctuation_regex = '[,.;"]+'
# 构建一个字典, key是单词, value是单词出现的文档编号
dictionary = {}

# 当前处理的文档编号
currentDocId = 0

# 语料库的文档总数
documents_total = len(documents)
# 文档的总词数, 用来记录每篇文档的总词数
documents_len = dict()

# 依次处理每篇文档
for d in documents:
    words = d.split()
    # 初始化每篇文档总词数
    words_count = 0

    for w in words:
        # 去标点
        w = re.sub(punctuation_regex, '', w.lower())
        if w in stopwords:
            continue
        elif w in dictionary:
            dictionary[w].append(currentDocId)
        else:
            dictionary[w] = [currentDocId]

        words_count += 1
    documents_len[currentDocId] = words_count
    currentDocId += 1

print(f"dictionary: {dictionary}")
print(f"语料库的文档总数documents_total: {documents_total}")
print(f"每篇文档的总词数documents_len: {documents_len}")

# tf = 某个词在文章中出现的次数 / 文章的总词数
# idf = log (语料库的文档总数 / (包含该词的文档数 + 1))
idf_dict = dict()
print(f"documents: {documents}")
import math
for k, v in dictionary.items():
    idf_dict[k] = math.log2(float(documents_total) / float((len(v) + 1)))

# 至少出现在两个文档中的单词选为关键词
keywords = [k for k in dictionary.keys() if len(dictionary[k]) > 1]
print(f'keywords: {len(keywords)}, {keywords}')
keywords.sort()
print(f'keywords: {len(keywords)}, {keywords}')

# 生成word-document矩阵[19, 13]
X = np.zeros([len(keywords), currentDocId])
print(f'X: {X}')
for i, k in enumerate(keywords):
    countWordDocument = {}
    for d in dictionary[k]:
        if d in countWordDocument:
            countWordDocument[d] += 1
        else:
            countWordDocument[d] = 1
    for d, v in countWordDocument.items():
        tf = float(v) / (documents_len[d])
        idf = idf_dict[k]
        tf_idf = tf / idf
        X[i, d] += tf_idf
        # X[i, d] += 1

print(f'X: {X}')

# 奇异值分解
U, sigma, V = linalg.svd(X, full_matrices=True)

print("U:\n", U.shape, "\n", U, "\n")
print("SIGMA:\n", sigma.shape, sigma, "\n")
print("V:\n", V.shape, V, "\n")

# 得到降维(降到targetDimension维)后单词与文档的坐标表示
targetDimension = 2
U2 = U[0:, 0:targetDimension]
V2 = V[0:targetDimension, 0:]
sigma2 = np.diag(sigma[0:targetDimension])

print(f"U.shape: {U.shape}, sigma.shape: {sigma.shape}, V.shape: {V.shape}")
print(f"U2.shape: {U2.shape}, sigma2.shape: {sigma2.shape}, V2.shape: {V2.shape}")

# 对比原始矩阵与降维结果
X2 = np.dot(np.dot(U2, sigma2), V2)
print("X:\n", X)
print("X2:\n", X2)

# 开始画图
pyplot.title("LSA")
pyplot.xlabel(u'x')
pyplot.ylabel(u'y')

# 绘制单词表示的点
# U2的每一行包含了每个单词的坐标表示(维度是targetDimension)，此处使用前两个维度的坐标画图
for i in range(len(U2)):
    pylab.text(U2[i][0], U2[i][1], keywords[i], fontsize=10)
    print("(", U2[i][0], ",", U2[i][1], ")", keywords[i])
x = U2.T[0]
y = U2.T[1]
pylab.plot(x, y, '.')

# 绘制文档表示的点
# V2的每一列包含了每个文档的坐标表示(维度是targetDimension)，此处使用前两个维度的坐标画图
Dkey = []
for i in range(len(V2[0])):
    pylab.text(V2[0][i], V2[1][i], ('D%d' % (i + 1)), fontsize=10)
    print("(", V2[0][i], ",", V2[1][i], ")", ('D%d' % (i + 1)))
    Dkey.append('D%d' % (i + 1))
x = V[0]
y = V[1]
pylab.plot(x, y, 'x')

pylab.savefig("tf-idf-svd.png", dpi=100)

exit()

机器学习分类维度一

• 有监督学习
• 无监督学习
• 半监督学习

机器学习分类维度二

• 分类
• 聚类
• 回归
• 关联规则

模型训练及测试

• 模型选择, 对特定任务最优建模方法的选择或者对特定模型最佳参数的选择
• 在训练数据集上运行模型(算法)并在测试数据集中测试效果, 迭代进行数据模型对修改, 这种方式称为交叉验证(将原始数据分为训练集和测试集, 使用训练集构建模型, 并使用测试集评估模型提供修改意见)
• 模型的选择会尽可能多的选择算法进行执行, 并比较执行结果
• 模型的测试一般从以下几个方面来进行比较, 分别是准确率, 召回率, 精准率, F值
  • 准确率(Accuracy) = 提取出的正确样本数/总样本数
  • 召回率(Recall) = 正确的正例样本数/样本中的正例样本数- 覆盖率
  • 精确度(Precision) = 正确的正例样本数/预测为正例的样本数
  • F值 = Precision Recall 2 / (Precision + Recall), 即F值是精准度和召回率的调和平均值

true positive(hit)真正例, 确实是正例
true negative(Correct Rejection)真负例, 确实是负例
false positive(False Alarm)假正例, 本来真实值是负例, 被预测为正例了, 虚报, 干扰报警
false negative(Miss)假负例, 本来真实值是正例, 被预测为负例了, 即没有预测出来

击中(Hit)(报准)和正确拒绝(Correct Rejection)是正确反应, 虚报(False Alarm)和漏报(Miss)是错误反应

A和D预测正确, B和C预测错误, 那么计算结果为:

举个例子, 真实值中, 正例为80, 负例为20; 预测值中, 正例为90, 负例为10, 然而, 在模型的实际预测中, 原本有75个真正的正例, 有15个是假正例, 5个假负例和5个真负例, 如下图所示:

Accuracy和Recall是一对互斥的关系, Accuracy在增大的时候Recall是在减小的

precision和accuracy的区别

ROC

ROC(Receiver Operating Characteristic), 描述的是分类混淆矩阵中FPR-TPR之间的相对变化情况.
纵轴是TPR(True Positive Rate), 横轴是FPR(False Positive Rate)

如果二元分类器输出的是对正样本对一个分类概率值, 当取不同阈值时会得到不同当混淆矩阵， 对应于ROC曲线上当一个点, ROC曲线就反应了FPR和TPR之间权衡当情况, 通俗的说, 即在TPR随着FPR递增的情况下, 谁增长的更快, 快多少的问题. TPR增长的越快, 曲线越往上弯曲, AUC就越大, 反应了模型的分类性能就越好. 当正负样本不平衡时, 这种模型评价方式比起一般当精确度评价方式的好处尤其显著.

AUC(Area Under Curve)

AUC被定义为ROC曲线下的面积, 显然这个面积的数值不会大于1. 由于ROC曲线一般都处于y=x这条直线的上方, 所以AUC的取之范围在0.5和1之间. AUC作为数值可以直观的评价分类器的好坏, 值越大越好.

AUC的值一般要求在0.7以上.

模型评估

回归结果度量

• explained_varicance_score, 可解释方差的回归评分函数
• mean_absolute_error, 平均绝对误差
• mean_squared_error, 平均平方误差

模型评估总结_分类算法评估方式

数据清洗和转换

• 实际生产环境中机器学习比较耗时的一部分
• 大部分机器学习模型所处理的都是特征, 特征通常是输入变量所对应的可用于模型的数值表示
• 大部分情况下, 收集到的数据需要经过预处理之后才能够被算法所用, 预处理的操作包括以下几个部分:
  • 数据过滤
  • 处理数据缺失
  • 处理可能的异常, 错误或异常值
  • 合并多个数据源数据
  • 数据汇总
• 对数据进行初步的预处理, 需要将其转换为一种适合机器学习模型的表示形式, 对许多模型来说, 这种表示就是包含数值数据的向量或者矩阵
  • 将类别数据编码成为对应的数值表示(一般使用1-of-k方法)-dumy
  • 从文本数据中提取有用的数据(一般使用词袋法或者TF-IDF)
  • 处理图像或者音频数据(像素, 声波, 音频, 振幅<傅立叶变换>)
  • 数值数据转换为类别数据以减少变量的值, 比如年龄分段
  • 对数值数据进行转换, 比如对数转换
  • 对特征进行正则化, 标准化, 以保证同一模型的不同输入变量的值域相同
  • 对现有变量进行组合或转换以生成新特征, 比如平均数, 可以做虚拟变量不断尝试

类型特征转换1-of-k(哑编码)

• 将非数值型的特征值转换为数值型的数据
• 假设变量的取值有k个, 如果对这些值用1到k编序, 则可用维度为k对向量来表示一个变量对值. 在这样的向量里, 该取值所对应的序号所在的元素为1, 其他元素均为0.

文本数据抽取

• 将一个文本当作一个无序的数据集合, 文本特征可以采用文本中的词条T进行体现, 那么文本中出现的所有词条及其出现的次数就可以体现文档的特征
• TF-IDF, 词条的重要性随着它在文件中出现的次数成正比增加, 但同时会随着它在语料库中出现的频率成反比下降;
  • 词条在文本中出现的次数越多, 表示该词条对该文本的重要性越高
  • 词条在所有文本中出现的次数越少, 说明这个词条对文本的重要性越高
  • TF(词频)指某个词条在文本中出现的次数, 一般会将其进行归一化处理(该词条数量/该文档中所有词条数量)
  • IDF(逆向文件频率)指一条词条重要性的度量, 一般计算方式为总文件数目除以包含该词语之文件的数目, 再将得到的商取对数得到. TF-IDF即TF*IDF

TF-IDF算法介绍及实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

from collections import defaultdict
import math
import operator


def loadDataSet():
    dataset = [ ['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],    # 切分的词条
                   ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                   ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                   ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                   ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                   ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid'] ]
    classVec = [0, 1, 0, 1, 0, 1]  # 类别标签向量，1代表好，0代表不好
    return dataset, classVec

def feature_select(list_words):
    doc_frequency = defaultdict(int)
    # print(type(doc_frequency))
    for word_list in list_words:
        for i in word_list:
            # print(doc_frequency[i])
            doc_frequency[i] += 1
            # print(doc_frequency[i])
            # print("===================")

    print(doc_frequency, doc_frequency.values())
    word_tf = {}
    for i in doc_frequency:
        word_tf[i] = doc_frequency[i] / sum(doc_frequency.values())
  
    doc_num = len(list_words)
    word_idf = {}
    word_doc = defaultdict(int)
    for i in doc_frequency:
        for j in list_words:
            if i in j:
                word_doc[i] += 1
    
    for i in doc_frequency:
        word_idf[i] = math.log(doc_num/(word_doc[i] + 1))


    word_tf_idf = {}
    for i in doc_frequency:
        word_tf_idf[i] = word_tf[i] * word_idf[i]

    # print(word_tf_idf)
    dict_feature_select = sorted(word_tf_idf.items(),key=operator.itemgetter(1),reverse=True)
    return dict_feature_select


if __name__=='__main__':
    data_list,label_list=loadDataSet() #加载数据
    # print(data_list, label_list)
    features=feature_select(data_list) #所有词的TF-IDF值
    print(features)
    print(len(features))

回归算法

回归算法是一种有监督算法,

• 线性回归
• Logistic回归
• Softmax回归
• 梯度下降
• 特征抽取
• 线性回归案例

回归算法认知

通过房屋面积预测房价, 如下图所示:

如果影响房价的还有房间数量, 那么:


那么问题的解决依赖于如下的方程:

最后就是要计算出$\theta$的值, 并选择最优的$\theta$值构成算法公式

那么它的似然函数为:

• 误差$\epsilon^{(i)}(i \le i \le n)$是独立同分布的, 服从均值为0, 方差为某定值$\sigma^2$的高斯分布(查看中心极限定理)
• 在实际中, 很多随机现象可以看作是众多因素的独立影响的综合反应, 往往服从正态分布

似然函数

当给定某个样本值x的时候, 那么得到的实际值y的概率是多少

上述只是一个样本, 概率越等于1越好, 如果对m个样本的概率进行相乘得到联合概率(样本与样本之间独立的), 这样就得到一个似然函数

对数似然, 目标函数及最小二乘法

$\theta$的求解过程

即让$J(\theta)$最小的时候, $\theta$的取值, 这就是最小二乘法

最小二乘法的参数最优解

• 参数解析式

  $$\theta = (X^TX)^{-1}X^TY$$

  X为特征矩阵, Y为目标属性, 如果一个矩阵可逆, 那么它的行列式大于0才可以

• 最小二乘法的使用要求矩阵$X^TX$是可逆的; 为了防止不可逆或者过拟合问题的存在, 可以增加额外的数据影响, 导致最终的矩阵是可逆的

  $$\theta = (X^TX + \lambda I)^{-1}X^TY$$

证明如下:

而$x^Tx$是半正定矩阵, 要想$\mu^TA\mu > 0$
而$\mu^Tx^Tx\mu + \mu^T\mu > 0$

那么中间的一定是大于0的, 就一定是正定矩阵，而正定矩阵是可逆的

另外一种理解方式

目标损失函数(loss/cost function)

• 0-1损失函数 $J(\theta) = \begin{cases}1, Y \ne f(X)\\ 0, Y = f(X) \end{cases}$
• 感知损失函数 $J(\theta) = \begin{cases}1, \vert Y - f(X) \vert > t\\ 0, \vert Y - f(X) \vert \leq t\end{cases}$
• 平方和损失函数 $$J(\theta) = \sum_{i=1}^{m}{(h_{\theta}(x^{(i)}) - y^{(i)})^2}$$
• 绝对值损失函数 $$J(\theta) = \sum_{i=1}^{m}{\vert h_{\theta}(x^{(i)}) - y^{(i)} \vert}$$
• 对数损失函数 $$J(\theta) = \sum_{i=1}^{m}{(y^{(i)}\log h_{\theta}(x^{(i)}))}$$

0-1损失函数在分类中用的比较多
感知损失函数用的也比较多, 稍微一变就是SVM
对数损失函数会用在逻辑回归中

误差

误差分为期望误差($L(f)$)和方差误差($\Omega(f)$)
偏差误差和方差之间的区别和联系

05.avi_30:00

多项式扩展就是将特征与特征之间进行融合，从而形成新的特征的一个过程; 从数学上来讲就是将低维度空间上的点映射到高维度空间中, 本身属于特征工程的一种操作.

如果模型在训练集上效果非常好, 而在训练集上效果不好, 那么认为这个时候存在过拟合的情况; 多项式扩展的时候, 如果指定的阶数比较大, 那么有可能导致过拟合, 从线性回归来讲, 认为训练出来的模型参数值越大, 就表示越存在过拟合的情况.

线性回归的过拟合

• 目标函数 $J(\theta) = \displaystyle \frac{1}{2}\displaystyle\sum_{i=1}^{m}{(h_\theta(x^{(i)}) - y^{(i)})^2}$
• 为了防止数据过拟合, 即$\theta$值的样本空间不能过大或者过小, 可以在目标函数增加一个平方和损失:
  $J(\theta) = \frac{1}{2}\displaystyle\sum_{i=1}^{m}{(h_\theta(x^{(i)}) - y^{(i)})^2} + \lambda \displaystyle\sum_{i=1}^{n}\theta_{j}^2$, 前面的一项体现的是期望误差, 后面一项体现的是模型的复杂度误差

• 正则项(norm): $\lambda \displaystyle\sum_{i=1}^{n}\theta_{j}^2$, 此正则项叫做L2-norm, 此外还有L1-norm: $\lambda \displaystyle\sum_{i=1}^{n}\vert \theta_{j} \vert$

  • L2-norm(Ridge回归, 岭回归): $J(\theta) = \frac{1}{2}\displaystyle\sum_{i=1}^{m}{(h_\theta(x^{(i)}) - y^{(i)})^2} + \lambda \displaystyle\sum_{i=1}^{n}\theta_{j}^2, \lambda > 0$
  • L1-norm(LASSO回归): $J(\theta) = \frac{1}{2}\displaystyle\sum_{i=1}^{m}{(h_\theta(x^{(i)}) - y^{(i)})^2} + \lambda \displaystyle\sum_{i=1}^{n}\vert \theta_{j} \vert, \lambda > 0$, LASSO回归中间很容易出现稀疏解, 即很多0的情况; L1-norm的求解方式为坐标轴下降法

为了解决过拟合问题, 可以选择在损失函数中加入惩罚项(对于系数过大的惩罚), 分为L1-norm和L2-norm

模型效果判断

• MSE, 误差平方和, 越趋近于0表示模型越拟合训练数据
• RMSE, MSE的平方根, 作用同MSE
• $R^2$, 取值范围$(-\infty, 1]$, 值越大表示模型越拟合训练数据; 最优解是1, 当模型预测为随机值的时候, 有可能为负; 若预测值恒为样本值期望, $R^2$为0
• TSS, 总平方和, 表示样本之间的差异情况, 是伪方差的m倍
• RSS, 残差平方和, 表示预测值和样本值之间的差异, 是MSE的m倍

Elastic Net

同时使用L1正则和L2正则的线性回归模型称为Elastic Net算法(弹性网络算法)

该公式中p表示选中L1-norm的概率是多少, 选中L2-norm的概率是多少

机器学习调参

• 实际中对于各种算法模型, 需要获取$\theta$, $\lambda$, $p$的值, $\theta$的求解其实就是算法模型的求解, 一般不需要开发人员的参与(算法已经实现), 主要需要求解的是$\lambda$和$p$的值(超参), 此过程叫做调参
• 交叉验证, 将训练数据分为多份, 其中一份进行数据验证并获取最优的超参$\lambda$和$p$, 比如十指交叉验证和五指交叉验证(scikit-learn中默认)

注: $y_i$为样本值, $\hat{y_i}$为预测值, $\overline{y_i}$为均值

梯度下降算法

• 目标函数$\theta$求解, $J(\theta) = \displaystyle \frac{1}{2}\displaystyle\sum_{i=1}^{m}{(h_{\theta}{(x^{(i)})} - y^{(i)})^2}$
• 初始化$\theta$(随机初始化, 可以初始化为0)
• 沿着负梯度方向迭代, 更新后的$\theta$使$J(\theta)$更小, $\theta = \theta - \alpha \cdot \displaystyle \frac{\partial J(\theta)}{\partial \theta}$, $\alpha$为学习率或者步长

求解如下:

批量梯度下降法(BGD)

随机梯度下降法(SGD)

线性回归的扩展

• 线性回归针对的是$\theta$而言, 对于样本本身, 样本可以是非线性的
  

局部加权回归

普通线性回归损失函数为:

局部加权回归损失函数为:

• $w^{(i)}$是权重, 根据预测的点与数据集中的点的距离来为数据集中的点赋权值, 当某点离要预测的点越远, 其权重越小, 否则越大. 常用值选择公式为: $$w^{(i)} = exp(- \frac{(x^{(i)} - \bar{x})^2}{2k^2})$$ 该函数为指数衰减函数, 其中$k$为波长参数, 它控制了权值随距离下降的速率

一般实际工作中, 当线性模型的参数接近0的时候, 我们认为当前参数对应的那个特征属性在模型判断中没有太大的决策信息, 所以对于这样的属性我们可以删除; 一般情况下, 如果是手动删除的话, 选择小于$1e-4$的特征属性

Logistic回归

Logistic/Sigmoid函数, $\displaystyle p = h_\theta(x) = g(\theta^Tx) = \frac{1}{1 + e^{-\theta^Tx}}$, p是个概率值

Logistic回归及似然函数

假设:

似然函数:

最大似然/极大似然函数的随机梯度
对数似然函数为:

Logistic回归$\theta$参数求解

极大似然估计与Logistic回归损失函数

Softmax回归

• softmax回归是logistic回归的一般化, 适用于K分类问题, 第K类的参数为向量$\theta_k$, 组成的二维矩阵为$\theta_{k \ast n}$
• softmax函数的本质是将一个K维的任意实数向量压缩(映射)成另一个K维的实数向量, 其中向量中的每个元素取值都介于(0, 1)之间
• softmax回归概率函数为: $$p(y=k|x;\theta) = \displaystyle \frac{e^{\theta_{k}^{T}x}}{\displaystyle \sum_{l=1}^{k}{e^{\theta_{l}^{T}x}}}, \quad k = 1, 2, ..., K$$

softmax算法原理

softmax算法损失函数

softmax算法梯度下降法求解

summary

• 线性模型一般用于回归问题, Logistic和 softmax模型一般用于分类问题
• 求$\theta$的主要方式是梯度下降法, 梯度下降法是参数优化的重要手段, 主要是SGD, 适用于在线学习以及跳出局部极小值
• Logistic和softmax回归是实践中解决分类问题的最重要的方法
• 广义线性模型对样本要求不必要服从正态分布, 只需要服从指数分布簇(二项分布, 泊松分布, 伯努利分布, 指数分布即可); 广义线性模型的自变量可以是连续的也可以是离散的

鸢尾花数据

参考案例

ravel和flatten

ravel是将多维数据转换为一维数据

线性回归+多项式扩展

• 如果数据本身不是线性关系, 那么直接使用线性回归模型效果不会体太好, 存在欠拟合
• 数据在低维空间中不是线性关系, 但是如果将数据映射到高维空间的时候, 数据就有可能变成线性关系, 从而就可以使用线性回归
• 如果映射的维度特别高, 那么数据就会完全变成线性的, 从而训练出来的模型会非常的契合训练数据; 但是实际上的数据可能会和训练数据存在一定的差距, 从而可能会导致模型在其他数据集上的效果不佳, 可能存在过拟合

过拟合

• 表现形式: 模型在训练集上效果非常好, 但是在测试集上效果不好
• 产生原因: 进入算法模型训练的这个数据集特别契合算法模型, 导致训练出来的模型非常完美, 但是实际的数据一定存在和训练集数据不一致的地方, 这个不一致就导致模型在其他数据集上效果不佳
• 解决方案: L1-norm和L2-norm

Logistic回归

• 本质上是一个二分类算法, 计算的是样本X属于一个类别的概率p, 样本属于另外一个类别的概率为1-p
• 最终认为样本X属于概率最大的那一个类别

  softmax回归

• 与Logistic回归的区别在于, softmax是一个多分类算法, 需要计算样本属于某一个类别的概率, 最终认为样本属于概率最大的那一个类别
• softmax会为每个类别训练一个参数$\theta$向量, 所以在softmax中需要求解的参数其实是一个由k个向量组成的$\theta$矩阵

持久化, 管道, 模型效果评估, 交叉验证

KNN

• 理论/原理: 认为”物以类聚, 人以群分”, 相同/近似样本在样本空间中是比较接近的, 所以可以使用和当前样本比较接近的的其他样本的目标属性作为当前样本的预测值
• 预测规则:
  • 分类: 多数投票或者加权多数投票
  • 回归: 平均值或者加权平均值
  • 权重一般选择是与距离成反比
• 相似度度量
  需要找相似的样本, 认为样本的特征向量在空间中的点之间的距离体现了样本之间的相似性, 越近的点越相似, 一般使用欧几里得距离
• 寻找最近邻的样本
  • 暴力的方式, 计算所有样本到当前样本的距离, 然后再获取最近的k个样本
  • KD-Tree方式, 通过构建KD-Tree, 减少计算量

决策树

集成学习

考虑: 虽然抽样数据在一定程度上体现了样本数据的特性, 所以我们用样本数据模型来预测它的全体数据. 但是数据与数据之间是存在一定的差异性的, 那么可以认为在当前数据集的模型有可能会出现不拟合生产环境中数据的情况 -> 过拟合;在决策树中, 进行划分特征属性选择的时候, 如果选择最优, 表示这个划分在当前数据集上一定是最优的, 但是不一定在全体数据集上最优; 在随机森林中, 如果每个决策树都是选择最优的进行划分的话, 就会导致所有子模型(内部的决策树)很大程度/概率上会使用相同的划分属性进行数据的划分, 就会特别容易导致过拟合, 所以在随机森林中, 选择划分属性的时候一般使用随机的方式选择

如果涉及到权重的话, 一般都是将错误率/正确率/距离/MSE/MAE等指标进行转换得到的

随机森林(Random Forest)推广算法

RF算法在实际应用中具有比较好的特性, 应用也比较广泛, 主要应用在分类, 回归, 特征转换, 异常点检测等, 常见的RF变种算法有:

• Extra Tree
• Totally Random Trees Embedding(TRTE)
• Isolation Forest

数学基础

常见函数

• 导数, 梯度
• Taylor展开, Taylor公式
• 概率论, 联合概率, 条件概率, 全概率公式, 贝叶斯公式
• 期望, 方差, 协方差
• 大数定理, 中心极限定理
• 估计法, 最大似然估计(MLE)
• 向量, 矩阵运算, 矩阵求导
• SVD, QR分解

梯度

梯度是一个向量, 表示某一个函数在该点处的方向导数沿着该方向取的最大值, 即函数在该点处沿着该方向变化最快, 变化率最大(即该梯度向量的模); 当函数为一维函数时, 梯度其实就是导数

Taylor公式

• Taylor公式是用一个函数在某点的信息描述其附近取值的公式. 如果函数足够平滑, 在已知函数在某一点的各阶导数值的情况下, Taylor公式可以利用这些导数值来做系数构建一个多项式近似函数在这一点的领域中的值.
• 若函数$f(x)$在包含$x_0$的某个闭区间$[a, b]$上具有$n$阶函数, 且在开区间$(a, b)$上具有$n+1$阶函数, 则对闭区间$[a, b]$上任意一点$x$, 有Taylor公式如下: $$f(x) = \frac{f(x_0)}{0!} + \frac{f^{'}(x_0)}{1!}(x-x_0) + \frac{f^{''}(x_0)}{2!}(x-x_0)^2 + ... + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n + R_n(x)$$

$f^{(n)}(x)$表示$f(x)$的$n$阶导数, $R_n(x)$是Taylor公式的余项, 是$(x-x_0)^n$的高阶无穷小

计算近似值, 并估计误差值

联合概率

两个事件同时发生的概率, 计作: $P(AB)$, $P(A, B)$, 或者$P(A \cap B)$, 即为”事件A和事件B同时发生的概率”

条件概率

事件A在另外一件事情B已经发生的条件下发生的概率叫做条件概率, 表示为P(A|B), 即为”在B条件下A发生的概率”
一般情况下, P(A|B) ≠ P(A)
条件概率有如下三个特性

• 非负性
• 可列性
• 可加性

如果将条件概率由两个事件推广到任意有穷多个事件时, 可以得到如下公式, 假设$A_1, A_2, …, A_n$为任意n个任意事件(n ≥ 2)), 而且$P(A_1A_2…A_n) > 0$, 则

即为, 事件$A_1$和事件$A_2$同时发生的概率等于事件$A_2$已经发生的条件下$A_1$发生的概率与事件$A_2$发生的概率的乘积

即为, 事件$A_2$和事件$A_1$同时发生的概率等于事件$A_1$已经发生的条件下$A_2$发生的概率与事件$A_1$发生的概率的乘积

即为, 事件$A_1$和事件$A_2$同时发生的概率

即为, 事件$A_2$已经发生的条件下$A_1$发生的概率与事件$A_2$发生的概率的乘积 等于 事件$A_1$已经发生的条件下$A_2$发生的概率与事件$A_1$发生的概率的乘积

全概率

样本空间$\Omega$有一组事件$A_1, A_2, …, A_n$, 如果事件组满足以下两个条件, 那么事件组称为样本空间的一个划分:

• $\forall i ≠ j \in \{1, 2, …, n\}, A_iA_j = \phi$
• $A_1 \cup A_2… \cup A_n = \Omega$

如果事件$\{A_j\}$是样本空间$\Omega$的一个划分, 且$P(A_j) > 0$, 那么对于任意事件B, 全概率公式为:

贝叶斯公式

设$A_1, A_2, …, A_n$是样本空间$\Omega$的一个划分, 如果对于任意事件B, 有$P(B) > 0$, 那么

概率公式总结

期望

期望即均值, 是概率加权下的”平均值”, 是每次可能结果的概率乘以其结果的总和, 反映的是随机变量平均取值大小, 常用符号$\mu$表示:

• 连续性数据, $E(X) = \int_{-\infty}^{+\infty}xf(x)dx$
• 离散性数据, $E(X) = \sum_{i}{x_ip_i}$

假设C为一个常数, X和Y是两个随机变量, 期望的性质如下:

• E(C) = C
• E(CX) = CE(X)
• E(X + Y) = E(X) + E(Y)
• 如果X和Y相互独立, 那么E(XY) = E(X)E(Y)
• 如果E(XY) = E(X)E(Y), 那么X和Y不相关

方差

衡量随机变量或一组数据离散程度的度量, 是用来度量随机变量和其数学期望之间的偏离程度. 即方差是衡量原数据和期望/均值相差的度量值.

假设C是一个常数, X和Y是两个随机变量, 那么方差的性质如下:

$D(C) = 0$
$D(CX) = C^2D(X)$
$D(C + X) = D(X)$
$D(X \pm Y) = D(X) + D(Y) \pm 2 Cov(X,Y)$

标准差

标准差(Standard Deviation)是方差的算术平方根, 用符号$\sigma$表示.
标准差和方差都是测量离散程度最重要最常见的指标. 不同之处在于标准差和变量的计算单位是相同的, 比方差清楚, 因此在很多分析的时候用标准差.

协方差

协方差常用于衡量两个变量的总体误差, 当两个变量相同的情况下, 协方差其实就是方差
如果X和Y是统计独立的, 那么二者之间的协方差为零; 如果协方差为零, 那么X和Y是不相关的.

假设C为一个常数, X和Y是两个随机变量, 那么协方差性质如下:

协方差是两个随机变量具有相同方向变化趋势的度量:

• 若$Cov(X, Y) > 0$, 则X和Y的变化趋势相同
• 若$Cov(X, Y) < 0$, 则X和Y的变化趋势相反
• 若$Cov(X, Y) = 0$, 则X和Y则不相关, 即变化没有什么相关性

对于n个随机向量($X_1, X_2, X_3…X_n$), 任意两个元素$X_i$和$X_j$都可以得到一个协方差, 从而形成一个n*n的矩阵即为协方差矩阵, 协方差矩阵为对称矩阵

大数定律

• 大数定律的意义在于, 随着样本容量n的增加, 样本平均数将接近于总体平均数(期望$\mu$), 所以在统计推断中, 一般都会使用样本平均数估计总体平均数的值.
• 使用一部分样本的平均值来代替整体样本的期望/均值, 出现偏差的可能是存在的, 但是当n足够大的时候, 偏差的可能性是非常小的, 当n无限大的时候, 这种可能性的概率基本为0
• 大数定律的作用就是为使用频率来估计概率提供来理论支持; 为使用部分数据来近似的模拟构建全部数据特征提供来理论支持

中心极限定理

• 中心极限定理(Central Limit Theorem), 假设${X_n}$为独立同分布的随机变量序列, 并有相同的期望$\mu$和方差$\sigma^2$, 则$X_n$服从中心极限定理, 且${Z_n}$为随机序列${X_n}$的规范和: $$Y_n = X_1 + X_2 + ... + X_n = \sum_{n=1}^{n}{X_i} \rightarrow N(n\mu, n\sigma^2)$$ $$Z_n = \frac{Y_n - E(Y_n)}{\sqrt{D(Y_n)}} = \frac{Y_n - n\mu}{\sqrt{n}\sigma} \rightarrow(0, 1)$$
• 中心极限定理就是一般在同分布的情况下, 抽样样本值的规范和在总体数量趋于无穷时的极限分布近似于正态分布

最大似然估计

• 最大似然估计(Maximum Likelihood Estimation, MLE)是一种具有理论性的参数估计方法. 基本思想: 当从模型总体随机抽取n组样本观测值后, 最合理的参数估计量应该使得从模型中抽取n组样本观测值的概率最大, 步骤如下:
  • 写出似然函数
  • 对似然函数取对数, 并整理
  • 求导数
  • 解似然函数

设总体分布为$f(x, \theta)$, $X_n$为该总体采样得到的样本. 因为随机序列${X_n}$独立同分布, 则它们的联合密度函数为:

• $\theta$被看作固定但是未知的参数, 反过来, 因为样本的已经存在, 可以看作${X_n}$是固定的, $L(x, \theta)$是关于$\theta$的函数, 即似然函数
• 求参数$\theta$, 使得似然函数取最大值, 此为最大似然估计法

似然与极大似然估计

向量的运算

两个向量: $\overrightarrow{a} = (x_1, y_1)$, $\overrightarrow{b} = (x_2, y_2)$, 并且a和b之间的夹角为$\theta$

• 数量积: 两个向量的数量积(内积, 点积)是一个数量/实数, 记作$\overrightarrow{a} \cdot \overrightarrow{b}$ $$\overrightarrow{a} \cdot \overrightarrow{b} = \vert \overrightarrow{a} \vert * \vert \overrightarrow{b} \vert * cos\theta$$
• 向量积: 两个向量的向量积(外积, 叉积)是一个向量, 记作$\overrightarrow{a} \times \overrightarrow{b}$; 向量积即两个不共线非零向量所在平面的一组法向量 $$\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert * \vert \overrightarrow{b} \vert * sin\theta$$

矩阵的运算

• 假设A, B均为$m*n$阶矩阵, 那么
  • $C = A \pm B$
  • $A + B = B +A$
  • $(A + B) + C = A + (B + C)$
  • $(\lambda\mu)A = \lambda(\mu A)$
  • $\lambda(A + B) = \lambda A + \lambda B$
  • $(AB)C = A(BC)$
  • $(A + B)C = AC + BC$
  • $C(A + B) = CA + CB$
  • $(A^T)^T = A$
  • $(\lambda A)^T = \lambda A^T$
  • $(AB)^T = B^TA^T$
  • $(A + B)^T = A^T + B^T$

QR分解

• QR分解是将矩阵分解为一个正交矩阵和一个上三角矩阵的乘积

• 其中, Q为正交矩阵, $Q^TQ = I, R为上三角矩阵$
• QR分解经常被用来解线性最小二乘问题

SVD分解

• 奇异值分解(Singular Value Decomposition)是一种重要的矩阵分解方法, 可以看作是对称矩阵在任意矩阵上的推广
• 假设A为一个$m*n$阶的实矩阵, 则存在一个分解使得: $$A_{m*n} = U_{m*n}\Sigma_{m*n}V_{m*n}^T$$
  • 通常奇异值由大到小排列, 这样$\Sigma$便能由A唯一确定了

向量的导数

A为一个$m*n$阶的矩阵, $x$为$n\ast1$的列向量, 则$Ax$为$m\ast1$的列向量, 计作$\overrightarrow{y} = A \cdot \overrightarrow{x}$

向量的导数

标量对向量的导数

• $A$为$n*n$的矩阵, $x$为$n \ast 1$的列向量, 计作$\overrightarrow{y} = \overrightarrow{x}^T \cdot A \cdot \overrightarrow{x}$
• 同理可得: $$\frac{\partial{y}}{\partial{\overrightarrow{x}}} = \frac{\partial(\overrightarrow{x}^T \cdot A \cdot \overrightarrow{x})}{\partial{\overrightarrow{x}}} = (A^T + A) \cdot \overrightarrow{x}$$
• 若A为对称矩阵, 则有 $$\frac{\partial(\overrightarrow{x}^T A \overrightarrow{x})}{\partial{\overrightarrow{x}}} = 2A\overrightarrow{x}$$ 推导过程如下:

由上式得到

标量对方阵对导数

A为$n * n$的矩阵, $|A|$为A的行列式, 计算$\frac{\partial{|A|}}{\partial{A}}$

模型训练及测试

• 模型选择, 对特定任务最优建模方法的选择或者对特定模型最佳参数的选择
• 在训练数据集上运行模型(算法)并在测试数据集中测试效果, 迭代进行数据模型对修改, 这种方式称为交叉验证(将原始数据分为训练集和测试集, 使用训练集构建模型, 并使用测试集评估模型提供修改意见)
• 模型的选择会尽可能多的选择算法进行执行, 并比较执行结果
• 模型的测试一般从以下几个方面来进行比较, 分别是准确率, 召回率, 精准率, F值
  • 准确率(Accuracy) = 提取出的正确样本数/总样本数
  • 召回率(Recall) = 正确的正例样本数/样本中的正例样本数- 覆盖率
  • 精确度(Precision) = 正确的正例样本数/预测为正例的样本数
  • F值 = Precision Recall 2 / (Precision + Recall), 即F值是精准度和召回率的调和平均值

true positive(hit)真正例, 确实是正例
true negative(Correct Rejection)真负例, 确实是负例
false positive(False Alarm)假正例, 本来真实值是负例, 被预测为正例了, 虚报, 干扰报警
false negative(Miss)假负例, 本来真实值是正例, 被预测为负例了, 即没有预测出来

击中(Hit)(报准)和正确拒绝(Correct Rejection)是正确反应, 虚报(False Alarm)和漏报(Miss)是错误反应

A和D预测正确, B和C预测错误, 那么计算结果为:

举个例子, 真实值中, 正例为80, 负例为20; 预测值中, 正例为90, 负例为10, 然而, 在模型的实际预测中, 原本有75个真正的正例, 有15个是假正例, 5个假负例和5个真负例, 如下图所示:

Accuracy和Recall是一对互斥的关系, Accuracy在增大的时候Recall是在减小的

precision和accuracy的区别

ROC

ROC(Receiver Operating Characteristic), 描述的是分类混淆矩阵中FPR-TPR之间的相对变化情况.
纵轴是TPR(True Positive Rate), 横轴是FPR(False Positive Rate)

如果二元分类器输出的是对正样本对一个分类概率值, 当取不同阈值时会得到不同当混淆矩阵， 对应于ROC曲线上当一个点, ROC曲线就反应了FPR和TPR之间权衡当情况, 通俗的说, 即在TPR随着FPR递增的情况下, 谁增长的更快, 快多少的问题. TPR增长的越快, 曲线越往上弯曲, AUC就越大, 反应了模型的分类性能就越好. 当正负样本不平衡时, 这种模型评价方式比起一般当精确度评价方式的好处尤其显著.

AUC(Area Under Curve)

AUC被定义为ROC曲线下的面积, 显然这个面积的数值不会大于1. 由于ROC曲线一般都处于y=x这条直线的上方, 所以AUC的取之范围在0.5和1之间. AUC作为数值可以直观的评价分类器的好坏, 值越大越好.

AUC的值一般要求在0.7以上.

模型评估

回归结果度量

• explained_varicance_score, 可解释方差的回归评分函数
• mean_absolute_error, 平均绝对误差
• mean_squared_error, 平均平方误差

模型评估总结_分类算法评估方式

有约束的最优化问题

• 最优化问题一般是指对于某一个函数而言, 求解在其指定作用域上的全局最小值问题, 一般分为三种情况, 这三种方法求出来的解都有可能有局部最小值, 只有当函数是凸函数的时候, 才可以得到全局最小值
  • 无约束问题, 一般求解方式为梯度下降法, 牛顿法, 坐标轴下降法, $ \displaystyle \min \limits_{x}f(x)$
  • 等式约束条件, 求解方式为拉格朗日乘子法, $\displaystyle \min \limits_{x}f(x), s.t: h_k(x)=0, k=1,2,\cdots, p$
  • 不等式约束条件, 求解方式为KKT条件 $$\displaystyle \min \limits_{x}f(x), s.t: h_k(x)=0, k=1,2,\cdots, p, g_j(x) \le 0, j=1, 2, \cdots, q$$

拉格朗日乘子法

对偶问题

在优化问题中, 目标函数f(x)存在多种形式, 如果目标函数和约束条件都为变量x的线性函数, 则称问题为线性规划; 如果目标函数为二次函数, 则称优化问题为二次规划; 如果目标函数或者约束条件为非线性函数, 则称最优化问题为非线性规划. 每个线性规划问题都有一个对偶问题

• 对偶问题的对偶是原问题
• 无论原始问题是否是凸的, 对偶问题都是凸优化问题
• 对偶问题可以给出原始问题的一个下界
• 当满足一定条件的时候, 原始问题和对偶问题的解是完美等价的

KKT条件

KKT条件是泛拉格朗日乘子法的一种形式, 主要应用在当我们的优化函数存在不等值约束的情况下的一种最优化解决方式; KKT条件即满足不等值约束的条件

KKT条件总结

• 拉格朗日取得可行解的充要条件, $\nabla_xL(x, \alpha, \beta) = 0$
• 将不等式约束转换后的一个约束, 称为松弛互补条件, $\beta_ig_i(x) = 0, \quad i=1,2,\cdots,q$
• 初始约束条件, $h_i(x)=0, \quad i=1,2,\cdots,p$
• 初始约束条件, $g_i(x)\le0,\quad i=1,2,\cdots,q$
• 不等式约束需要满足的条件, $\beta_i\ge0,\quad i=1,2,\cdots,q$