梯度下降

梯度下降

梯度下降是常用的卷积神经网络模型参数的求解方法, 根据每次参数更新使用样本数量的多少, 可以分为以下三类:

• 批量梯度下降(batch gradient descent, BGD)
• 小批量梯度下降(mini-batch gradient descent, MBGD)
• 随机梯度下降(stochastic gradient descent, SGD)

求参数过程即最小化损失函数过程, 比如有一个含有D个训练数据的数据集, 损失函数为:

$$L(W) = \displaystyle \frac{1}{\vert D \vert} \sum_{i}^{\vert D \vert} f_W(x^{(i)}) + \lambda \gamma(W)$$

$f_W(X^{(i)})$是单个样本$X^{(i)}$的损失, $\gamma(W)$是正则项, $\lambda$是权重

批量梯度下降

量梯度下降(batch gradient descent, BGD), 是梯度下降法最原始的形式, 具体思路是在更新每一组参数的时候都使用所有的样本进行更新, 如果是几百万个样本集的话, 训练时间和内存将都不可取

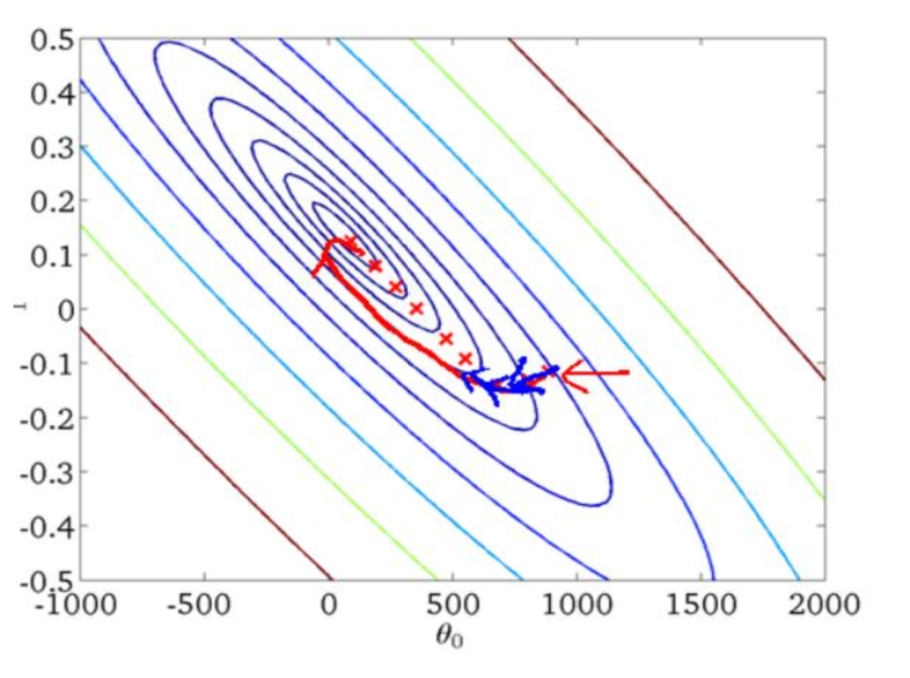
随机梯度下降

随机梯度下降(stochastic gradient descent, SGD), 是为了解决批量梯度下降法在训练过程中随着样本数量的增加而变得异常缓慢的问题提出的

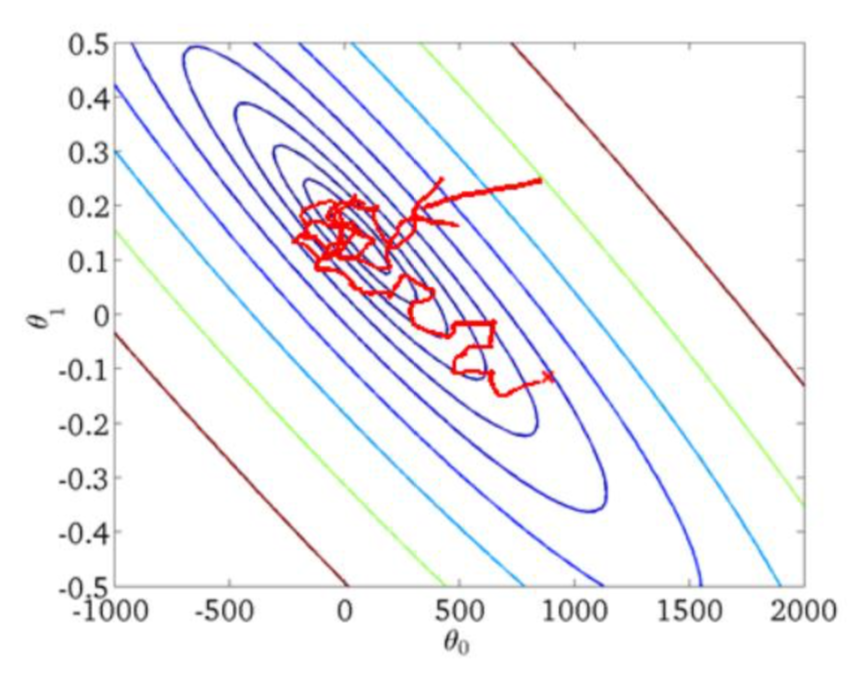
小批量梯度下降

批量梯度下降和随机梯度下降都有各自的优缺点, 不能取得性能和准确率之间的平衡, 而小批量梯度下降(mini-batch gradient descent, MBGD), 是在每次更新参数时时使用b个样本(b一般为较小的数, 如100)

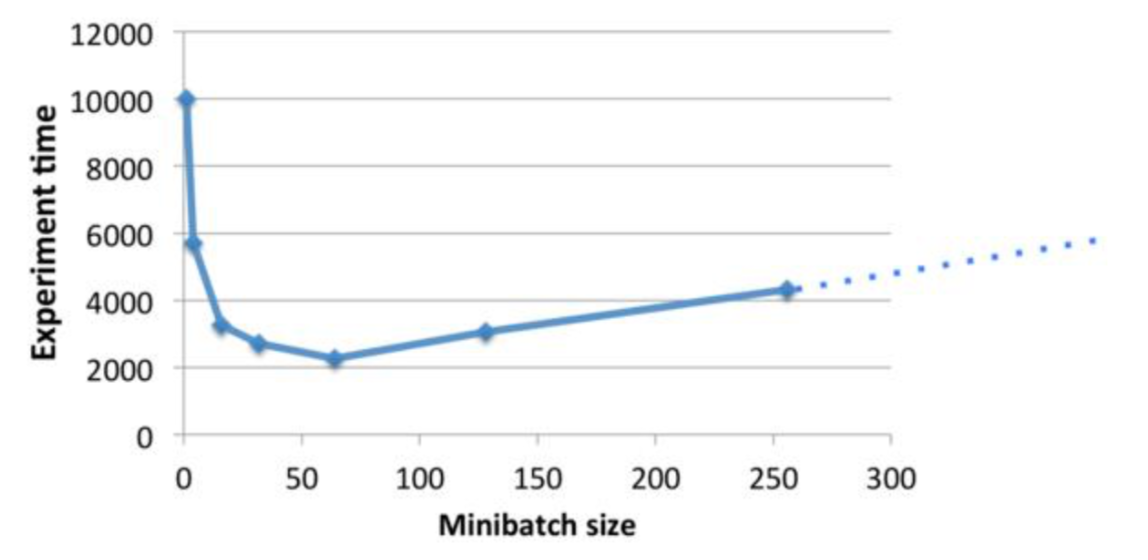
梯度下降法_L8

梯度下降法(Gradient Descent, GD)常用于求解无约束情况下凸函数(Convex Function)的极小值, 是一种迭代类型的算法, 因为凸函数只有一个极值点, 故求解出来的极小值就是函数的最小值点

$$J(\theta) = \frac{1}{2m} \displaystyle \sum_{i=1}^m ( h_\theta(x^{(i)}) - y^{(i)} )^2$$ $$\theta^\ast = arg \min \limits_{\theta} J(\theta)$$

导数: 一个函数在某一点的导数描述类这个函数在这一点附近的变化率, 也可以认为是函数在某一点的导数就是该函数所代表的曲线在这一点的切线斜率. 导数值越大, 表示函数在该点处的变化越大.

梯度: 梯度是一个向量, 表示某一函数在该点处的方向导数沿着该方向取的最大值, 即函数在该点处沿着该方向变化最快, 变化率最大(即该梯度向量的模); 当函数为一维函数的时候, 梯度就是导数

$$y' = \frac{\partial f(x)}{\partial x}$$ $$\nabla f(x_1, x_2) = ( \frac{ \partial f(x_1, x_2) }{\partial x_1}, \frac{\partial f(x_1, x_2)}{\partial x_2})$$

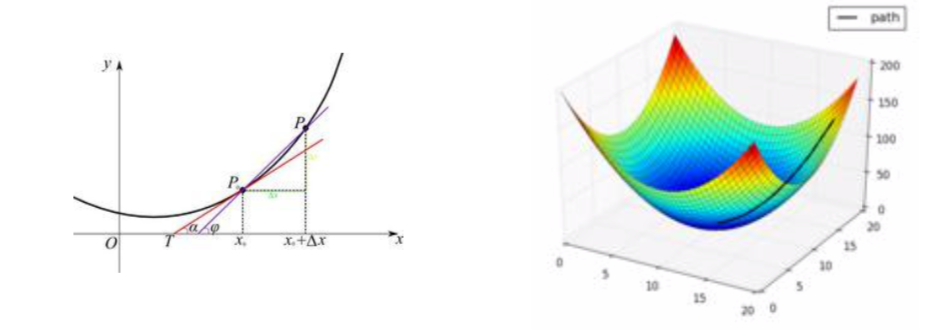
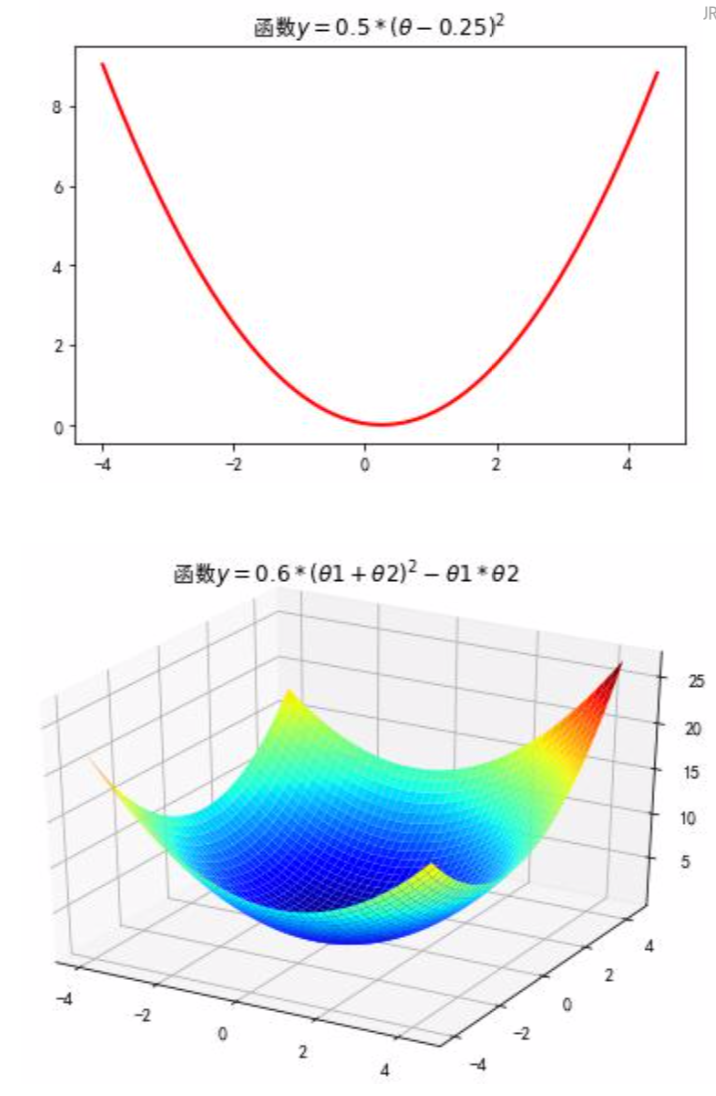
梯度下降法的优化思想是用当前位置负梯度方向作为搜索方向, 因为该方向为当前位置的最快下降方向, 所以梯度下降法也称为”最速下降法”. 梯度下降法中越接近目标值, 变量变化越小, 如下:

$$\theta^{k+1} = \theta^k - \alpha \nabla f(\theta^k)$$

$\alpha$称为步长或者学习率(learning rate), 表示自变量$x$每次迭代变化的大小

收敛条件: 当目标函数的函数值变化非常小的时候或者达到最大迭代次数的时候, 就结束循环

由于梯度下降法中负梯度方向作为变量的变化方向, 所有有肯能导致最终解的值是局部最优解, 所以在使用梯度下降的时候, 一般需要进行一些调优策略

• 学习率的选择: 学习率过大, 表示每次迭代更新的时候变化比较大, 有可能会跳过最优解; 学习率过小, 表示每次迭代更新的时候变化比较小, 就会导致迭代速度过慢, 很长时间都不能结束
• 算法初始参数值的选择: 初始值不同, 最终获得的最小值也有可能不同, 因为梯度下降法求解的是局部最优解, 所以一般情况下, 选择多次不同初始值运行算法, 并最终返回损失函数最小情况下的结果值
• 标准化: 由于样本不同特征的取值范围不同, 可能导致在各个不同参数上迭代速度不同, 为了减少特征取值的影响, 可以将特征进行标准化操作

批量梯度下降法(Batch Gradient Descent, BGD)

使用所有样本在当前点的梯度值对变量参数进行更新操作

$$\theta^{k+1} = \theta^k - \alpha \displaystyle \sum_{i=1}^m \nabla f_{\theta^k} (x_i)$$

随机梯度下降法(Stochastic Gradient Descent, SGD)

在更新变量参数的时候, 选取一个样本的梯度值来更新参数

$$\theta^{k+1} = \theta^k - \alpha \nabla f_{\theta^k} (x_i)$$

小批量梯度下降法(Mini-batch Gradient Descent, MBGD)

集合BGD和SGD的特性, 从原始数据中, 每次选择n个样本来更新参数值, 一般n选择10

$$\theta^{k+1} = \theta^k - \alpha \displaystyle \sum_{i=t}^{t+n-1} \nabla f_{\theta^k} (x_i)$$

BGD/SGD/MBGD的区别

• 当样本量为m的时候, 每次迭代BGD算法中对于参数值更新一次, SGD算法中对于参数值更新m次, MBGD算法中对于参数值更新$m/n$次, 相对来讲SGD算法的更新速度最快
• SGD算法中对于每个样本都需要更新参数值, 当样本值不太正常的时候, 就有可能会导致本次的参数更新会产生相反的影响, 也就是说SGD算法的结果并不是完全收敛的, 而是在收敛结果处波动的
• SGD算法是每个样本都更新一次参数值, 所以SGD算法特别适合样本数据量大的情况以及在线机器学习(Online ML)