20191207

如何用极大似然概率解释交叉熵loss

Logistic回归

Logistic/Sigmoid函数, $\displaystyle p = h_\theta(x) = g(\theta^Tx) = \frac{1}{1 + e^{-\theta^Tx}}$, p是个概率值

$$g(z) = \frac{1}{1 + e^{-z}}$$ $$\begin{align} g^\prime(z) = &(\frac{1}{1 + e^{-z}})^\prime = \frac{e^{-z}}{(1 + e^{-z})^2}\\ &=\frac{1}{1 + e^{-z}} \cdot \frac{e^{-z}}{(1 + e^{-z})} = \frac{1}{1 + e^{-z}} \cdot (1 - \frac{1}{1 + e^{-z}})\\ &=g(z) \cdot (1 - g(z))\\ \end{align}$$ $$y = \begin{cases}0\\ 1\end{cases}$$ $$\hat{y} = \begin{cases}1, P(\hat{y} = 1) > p\\ 0, P(\hat{y} = 0) > p\end{cases}$$

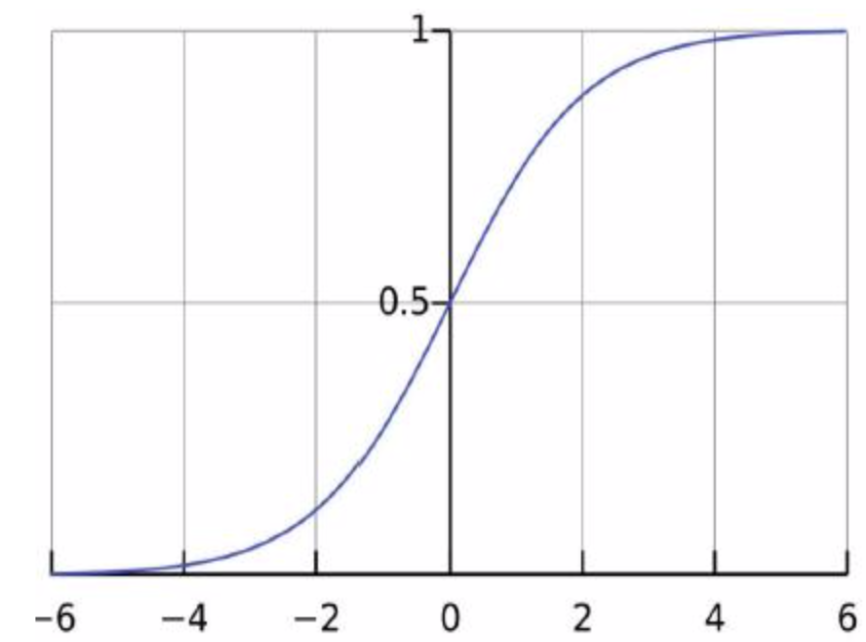
Logistic回归及似然函数

	y=1	y=0
$p(y \mid x)$	$\theta$	$1 - \theta$

假设:

$$P(y=1|x;\theta) = h_\theta(x)$$ $$P(y=0|x;\theta) = 1 - h_\theta(x)$$ $$P(y|x;\theta) = h_\theta(x) \ast (1 - h_\theta(x)) = (h_\theta(x))^y(1 - h_\theta(x))^{(1-y)}$$

似然函数:

$$\begin{align}L(\theta) &= p(\overrightarrow y \mid X;\theta) = \displaystyle \prod_{i=1}^{m}{p(y^{(i)}|x^{(i)}; \theta)}\\ &=\displaystyle \prod_{i=1}^{m} (h_\theta(x^{(i)}))^y{^{(i)}}(1 - h_\theta(x^{(i)}))^{(1-y^{(i)})}\\ \end{align}$$

最大似然/极大似然函数的随机梯度
对数似然函数为:

$$l(\theta) = logL(\theta) = \displaystyle \sum_{i=1}^{m}(y^{(i)}log h_\theta(x^{(i)}) + (1 - y^{(i)})log(1 - h_\theta(x^{(i)})))$$

极大似然估计与Logistic回归损失函数

$$L(\theta) = \displaystyle \prod_{i=1}^{m}{p(y^{(i)}|x^{(i)}; \theta)} = \displaystyle \prod_{i=1}^{m}{p_{i}^{y^{(i)}}(1-p_i)^{(1-y^{(i)})}}, \quad p_i = h_\theta(x^{(i)}) = \frac{1}{1 + e^{\displaystyle - \theta^{T} x^{(i)}}}$$ $$l(\theta) = lnL(\theta) = \displaystyle \sum_{i=1}^{m} ln[p_{i}^{y^{(i)}}(1-p_i)^{(1-y^{(i)})}]$$ $$\begin{align}loss &= - l(\theta)\\ &= - \displaystyle \sum_{i=1}^{m}[y^{(i)}ln(p_i) + (1-y^{(i)})ln(1-p_i)] \\ \end{align}$$

如果我们对m个样本取平均, 得到如下:

$$- \frac{1}{m} \displaystyle \sum_{i=1}^{m}[y^{(i)}ln(p_i) + (1-y^{(i)})ln(1-p_i)]$$

即cross entropy

详情参考

硬币问题为何不使用MLP而直接假设正反面概率p?

1. 对于硬币游戏, 硬币只有正面和反面两种情况, 那么对于同一个硬币来说, 正面的概率是$p$的话, 那么反面的概率就是$1-p$, 根据一个已知的硬币观测序列, 可以直接将观测到的正反面情况带入相应的概率公式, 通过梯度下降得到极值;
2. 而MLP分为输入层, 隐藏层, 输出层, 层级之间使用全连接, 需要将特征值传入进去, 通过带有结果的数据来训练神经网络的weight和bias, 本质上是将线性不可分的数据通过增加隐藏层构造切分平面使之线性科锋, 解决的问题基本上是分类问题.

面对未知分类问题，存在A,B,C三个模型，如何确定使用哪一个模型？

• 模型选择, 对特定任务最优建模方法的选择或者对特定模型最佳参数的选择
• 在训练数据集上运行模型(算法)并在测试数据集中测试效果, 迭代进行数据模型对修改, 这种方式称为交叉验证(将原始数据分为训练集和测试集, 使用训练集构建模型, 并使用测试集评估模型提供修改意见)
• 模型的选择会尽可能多的选择算法进行执行, 并比较执行结果
• 模型的测试一般从以下几个方面来进行比较, 分别是准确率, 召回率, 精准率, F值
  • 准确率(Accuracy) = 提取出的正确样本数/总样本数
  • 召回率(Recall) = 正确的正例样本数/样本中的正例样本数- 覆盖率
  • 精确度(Precision) = 正确的正例样本数/预测为正例的样本数
  • F值 = Precision Recall 2 / (Precision + Recall), 即F值是精准度和召回率的调和平均值

		预测值
		正例	负例
真实值	正例	true positive真正例(A)	false negative假负例(B)
	负例	false positive假正例(C)	true negative真负例(D)

true positive(hit)真正例, 确实是正例
true negative(Correct Rejection)真负例, 确实是负例
false positive(False Alarm)假正例, 本来真实值是负例, 被预测为正例了, 虚报, 干扰报警
false negative(Miss)假负例, 本来真实值是正例, 被预测为负例了, 即没有预测出来

击中(Hit)(报准)和正确拒绝(Correct Rejection)是正确反应, 虚报(False Alarm)和漏报(Miss)是错误反应

A和D预测正确, B和C预测错误, 那么计算结果为:

$$Accuracy = (A + D) / (A + B + C + D)$$ $$Recall = A / (A + B)$$ $$Precision = A / (A + C)$$ $$\displaystyle F = \frac{Precision \ast Recall \ast 2}{Precision + Recall}$$

举个例子, 真实值中, 正例为80, 负例为20; 预测值中, 正例为90, 负例为10, 然而, 在模型的实际预测中, 原本有75个真正的正例, 有15个是假正例, 5个假负例和5个真负例, 如下图所示:

		预测值
		正例90	负例10
真实值	正例80	真正例(A)75	假负例(B)5
	负例20	假正例(C)15	真负例(D)5

Accuracy和Recall是一对互斥的关系, Accuracy在增大的时候Recall是在减小的

ROC

ROC(Receiver Operating Characteristic), 描述的是分类混淆矩阵中FPR-TPR之间的相对变化情况.
纵轴是TPR(True Positive Rate), 横轴是FPR(False Positive Rate)

如果二元分类器输出的是对正样本对一个分类概率值, 当取不同阈值时会得到不同当混淆矩阵， 对应于ROC曲线上当一个点, ROC曲线就反应了FPR和TPR之间权衡当情况, 通俗的说, 即在TPR随着FPR递增的情况下, 谁增长的更快, 快多少的问题. TPR增长的越快, 曲线越往上弯曲, AUC就越大, 反应了模型的分类性能就越好. 当正负样本不平衡时, 这种模型评价方式比起一般当精确度评价方式的好处尤其显著.

AUC(Area Under Curve)

AUC被定义为ROC曲线下的面积, 显然这个面积的数值不会大于1. 由于ROC曲线一般都处于y=x这条直线的上方, 所以AUC的取之范围在0.5和1之间. AUC作为数值可以直观的评价分类器的好坏, 值越大越好.

AUC的值一般要求在0.7以上.

模型评估

回归结果度量

• explained_varicance_score, 可解释方差的回归评分函数
• mean_absolute_error, 平均绝对误差
• mean_squared_error, 平均平方误差

模型评估总结_分类算法评估方式

指标	描述	scikit-learn函数
Precision	精确度	from sklearn.metrics import precision_score
Recall	召回率	from sklearn.metrics import recall_score
F1	F1指标	from sklearn.metrics import f1_score
Confusion Matrix	混淆矩阵	from sklearn.metrics import confusion_matrix
ROC	ROC曲线	from sklearn.metrics import roc
AUC	ROC曲线下的面积	from sklearn.metrics import auc
Mean Square Error(MSE, RMSE)	平均方差	from sklearn.metrics import mean_squared_error
Absolute Error(MAE, RAE)	平均方差	from sklearn.metrics import mean_absolute_error, median_absolute_error
R-Squared	平均方差	from sklearn.metrics import r2_score