L7

回顾

决策树和集成学习

• 分类决策树和回归决策树

• 决策树的构建

  • 目的: 让同一个类别/y的取值接近的样本在同一个叶子节点中, 让一个叶子节点中的样本足够的”纯”
  • “纯”的度量方式(值越大表示数据越不”纯”)
    • 信息熵(分类)
    • gini系数(分类)
    • 错误率(分类)
    • MSE(回归)
    • MAE(回归)
  • 进行数据划分的特征属性的选择
    • 基于划分前”纯”度的指标和划分后”纯”度值之间的差距, 作为特征属性的选择, 叫做信息增益, 选择增益越大的特征属性作为最终的划分数据
      基于划分前”纯”度的指标和划分后”纯”度值之间的差距, 然后相对于划分属性的”纯”度值的比率, 作为特征属性选择的依据, 叫做信息增益率, 选择增益率最大的特征属性作为最终的划分属性
  • 数据的划分方式
    • 对于离散数据, 如果是构建多叉树, 那么此时一个特征的取值就是一个分支
    • 对于离散数据, 如果是构建二叉树, 那么将离散数据转换为”属于该值”和”不属于该值”两个类别, 然后再每个类别一个分支
    • 对于连续数据, 在连续数据中找出一个split_point点, 然后让大于等于split_point的数据属于一个分支, 让其他数据属于另外一个分支

• 决策树的预测

• 欠拟合和过拟合

  • 欠拟合解决方案: 可以通过增加树的层次来解决这个问题, 但是如果层次足够高的话又会导致过拟合
  • 过拟合解决方案: 剪枝(前剪枝和后剪枝), 或者多棵树的集成学习(随机森林), 在选择划分的特征属性的时候不进行全局最优选择, 而是进行局部最优选择

• 常见的算法

  • ID3
  • C4.5
  • CART

• 集成学习

  • 思路, 将多个模型进行融合, 使用融合后的结果作为真实的预测值
  • bagging, 对数据进行重采样, 然后使用重采样的数据进行模型训练, 然后将训练的多个模型预测结果进行融合; 如果是分类就多数投票或者加权的多数投票, 如果是回归就均值或者加权均值
    • 代表算法是随机森林

  • boosting, 对训练数据进行更改(样本权重的更改, 或者样本数据值的更改), 然后使用更改后的数据来训练模型, 训练之后对模型进行加权的操作

    • 代表算法有两种, adaboost基于样本的权重进行模型构建, 权重越高的样本在模型训练的时候起到的决策性作用越大; 样本的更新规则, 如果一个样本被前面的模型预测错误, 那么当前这个样本的权重就增大; 模型的权重给定规则, 如果一个模型的预测越准确, 模型的权重越高
    • adaboost本质是每次迭代构建模型的时候, 对于之前分类错误的样本着重考虑
    • GBDT, 梯度提升树, 在每次迭代的时候使用上一次的训练数据和上一次训练之后模型的预测值之间的残差作为当前模型的输入
    • GBDT本质, 每次迭代模型的时候, 都是在之前模型预测的结果的基础上进行预测, 每次产生的模型都让误差/偏度变得更小
    • GBDT中所有模型权重相同
    • 衰减因子, 每次考量模型的时候, 不是完全的相信模型效果, 所以可以对模型进行一个缩放操作; 每次更新的时候不是基于全部的预测值(y_true - y_predict), 而是采用变化一小点的策略(y_true - alpha * y_predict)

  • stacking

    • 使用原始数据和算法模型(不要求一样)训练多个模型
    • 使用第一步训练的多个模型在训练集上的预测值组成一个特征举证X, 使用原始数据中的目标属性作为Y, 然后再训练一个模型, 就相当于模型的算法集成, 而不是通过数据上的算法集成

聚类算法

课程内容

• Jaccard相似度, Pearson相似度
• K-means聚类
• 聚类算法效果评估(准确率, 召回率等)
• 层次聚类算法
• 密度聚类算法
• 谱聚类算法

什么是聚类

聚类就是对大量未知标注对数据集, 按照数据内部存在的数据特征将数据划分为多个不同的类别, 使类别内的数据比较相似, 类别之间的数据相似度比较小; 属于无监督学习

聚类算法的重点是计算样本项之间的相似度, 有时候也称为样本间的距离

和分类算法的区别

• 分类算法属于有监督学习, 基于有标注的历史数据进行算法模型构建
• 聚类算法属于无监督学习, 数据集中的数据是没有标注的

相似度/距离公式

闵可夫斯基距离(Minkovski)

$$dist(X, Y) = \displaystyle \sqrt[p]{ \sum_{i=1}^n \vert x_i - y_i \vert^p}$$

• 当p为1的时候就是曼哈顿距离(Manhattan) $$M_{dist} = \displaystyle \sum_{i=1}^n \vert x_i - y_i \vert$$
• 当p为2的时候就是欧式距离(Euclidean) $$E_{dist} = \displaystyle \sqrt{ \displaystyle \sum_{i=1}^n (x_i - y_i)^2}$$
• 当p为无穷大的时候就是切比雪夫距离(Chebyshev) $$C_{dist} = \max \limits_{i} ( \vert x_i - y_i \vert )$$

标准化欧式距离(Standardized Euclidean Distance)

$$X^{\ast} = \frac{ X - \bar X}{s}$$ $$s = \sqrt{ \frac{ \displaystyle \sum_{i=1}^n (x_i - y_i)^2}{n} }$$ $$S\_E\_D = \sqrt{ \displaystyle \sum_{i=1}^n (\frac{x_i - y_i}{s_i})^2 }$$

夹角余弦相似度(Cosine)

$$a = (x_{11}, x_{12}, \cdots, x_{1n})$$ $$b = (x_{21}, x_{22}, \cdots, x_{2n})$$ $$cos(\theta) = \displaystyle \frac{\displaystyle \sum_{k=1}^n x_{1k} x_{2k}}{\sqrt{\displaystyle \sum_{k=1}^n x_{1k}^2} \ast \sqrt{\displaystyle \sum_{k=1}^n x_{2k}^2}} = \frac{a^T \cdot b}{\vert a \vert \vert b \vert}$$

KL距离(相对熵)

$$D(P \Vert\Vert Q) = \sum_x P(x) log(\frac{P(x)}{Q(x)})$$

杰卡德相似系数(Jaccard)

$$J(A, B) = \frac{\vert A \bigcap B \vert}{\vert A \bigcup B \vert}, \quad dist(A, B) = 1 - J(A, B) = \frac{\vert A \bigcup B \vert - \vert A \bigcap B \vert}{\vert A \bigcup B \vert}$$

Pearson相关系数

$$\rho_{XY} = \frac{Cov(X, Y)}{\sqrt{D(X)} \sqrt{D(Y)}} = \frac{ E[(X-E(X))(Y-E(Y)) ]} {\sqrt{D(X)} \sqrt{D(Y)}}= \frac{ \displaystyle \sum_{i=1}^n (X_i - \mu_X)(Y_i - \mu_Y) }{\sqrt{\displaystyle \sum_{i=1}^n (X_i - \mu_X)^2} \ast \sqrt{\displaystyle \sum_{i=1}^n (Y_i - \mu_Y)^2}}$$ $$dist(X, Y) = 1 - \rho_{XY}$$

聚类的思想

给定一个有M个对象的数据集, 构建一个具有k个簇的模型, 其中$k \le M$, 满足以下条件:

• 每个簇至少包含一个对象
• 每个对象属于且仅属于一个簇
• 将满足上述条件的k个簇称为一个合理的聚类划分

基本思想: 对于给定的类别数据k, 首先给定初始划分, 通过迭代改变样本和簇的隶属关系, 使得每次处理后的得到的划分比上一次的好(总的数据集之间的距离和变小了)

K-means算法

K-means算法, 也称为K平均或者K均值, 是使用广泛的最基础的聚类算法

假设输入样本为$T=X_1, X_2, \cdots, X_m$, 则算法步骤(使用欧几里得距离公式)为:

• 选择初始化的k个类别中心$a_1, a_2, \cdots, a_k$
• 对于每个样本$X_i$, 将其标记为距离类别中心$a_j$最近的类别j
• 更新每个类别的中心点$a_j$为隶属于该类别的所有样本的均值
• 重复上述两步操作, 直到达到某个终止条件

终止条件

• 迭代次数, 最小平方误差MSE, 簇中心点变化率

$$label_i = arg \min \limits_{1 \le j \le k} { \sqrt{ \displaystyle \sum_{i=1}^n (x_i - a_j )^2 } }$$ $$a_j = \frac{1}{N(c_j)} \sum_{i \in c_j}x_i$$

K-means算法过程

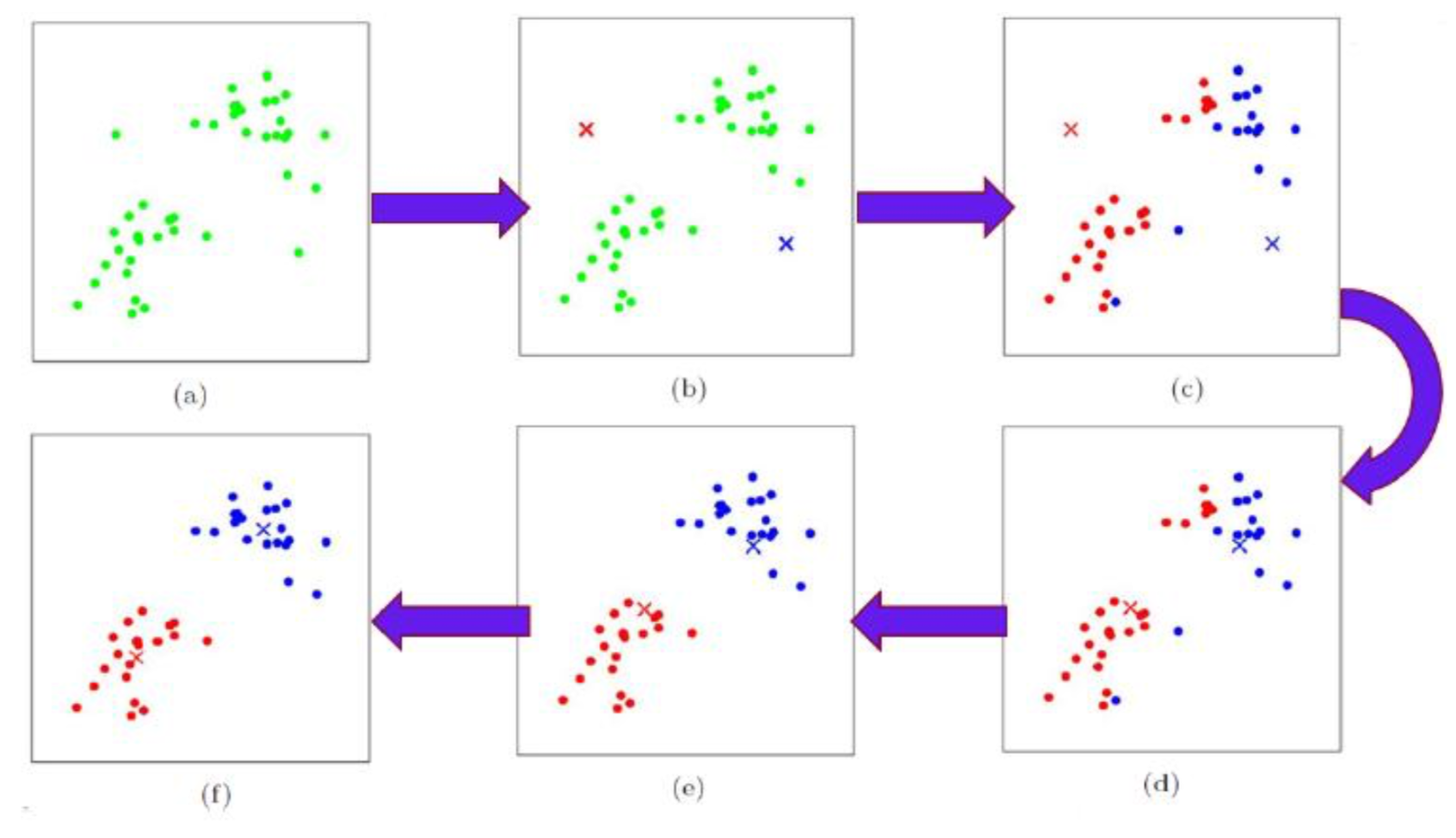
记K个簇中心分别为$a_1, a_2, \cdots, a_K$, 每个簇的样本数量为$N_1, N_2, \cdots, N_K$
使用平方误差作为目标函数(使用欧几里得距离), 公式为:

$$J(a_1, a_2, \cdots, a_K) = \frac{1}{2} \displaystyle \sum_{j=1}^K \sum_{i=1}^{N_j} ( \overrightarrow {x_i} - \overrightarrow {a_j})^2$$

要获取最优解, 即使得目标函数尽可能的小, 对函数J求偏导, 可以得到簇中心点a更新对公式:

$$\frac{\partial J}{\partial a_j} = \displaystyle \sum_{i=1}^{N_j} (x_i - a_j) \underrightarrow{令} 0 \Rightarrow a_j = \frac{1}{N_j} \sum_{i=1}^{N_j} x_i$$

K-means算法在迭代过程中使用所有点的均值作为新的质心(中心点), 如果簇中存在异常点, 将导致均值偏差比较严重
比如一个簇中有2, 4, 6, 8, 100五个数据, 那么新的质心为24, 显然这个质心离绝大多数点都比较远, 在当前情况下, 使用中位数6可能比使用均值的想法更好, 使用中位数的聚类方法叫做K-Mediods聚类(K中值聚类)

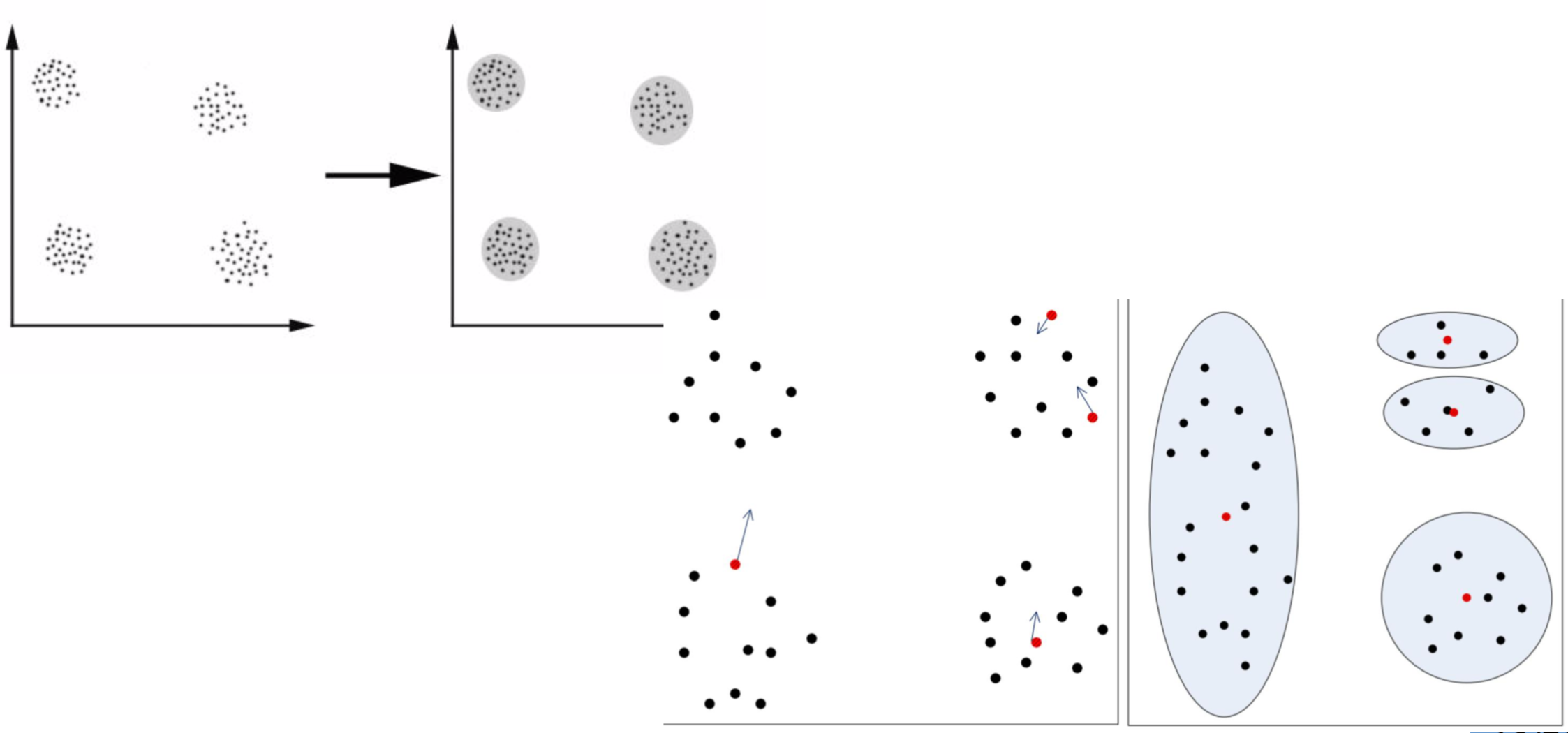
K-means算法初值敏感

K-means算法是初值敏感的, 选择不同的初始值可能导致不同的簇划分规则, 为了避免初值敏感最终导致的结果异常, 可以采用初始化多套初始节点构造不同的分类规则, 然后选择最优的构造规则

K-means算法初优缺点

缺点:

• K值是用户给定的, 在进行数据处理前, K值是未知的, 不同的K值得到的结果也不一样
• 对初始簇中心点是敏感的
• 不适合发现非凸形状的簇或者大小差别较大的簇
• 特殊值(离群值)对模型的影响比较大

优点:

• 理解容易, 聚类效果不错
• 处理大数据集的时候, 该算法可以保证较好的伸缩性和高效率
• 当簇近似高斯分布的时候, 效果非常不错

K-means算法案例

二分K-means算法

解决K-means算法对初始簇中心比较敏感的问题, 二分K-means算法是一种弱化初始质心的一种算法, 具体思路步骤如下:

• 将所有样本数据作为一个簇放到一个队列中
• 从队列中选择一个簇进行K-means算法划分, 划分为两个簇, 并将子簇添加到队列中
• 循环迭代第二步操作, 知道终止条件达到(聚簇数量, 最小平方误差, 迭代次数)
• 队列中的簇就是最终的分类簇集合

从队列中选择划分聚簇的规则一般有两种方式:

• 对所有簇计算误差和SSE(SSE也可以认为是距离函数的一种变种), 选择SSE最大的聚簇进行划分操作(优先这种策略)
• 选择样本数据量最多的簇进行划分操作

$$SSE = \displaystyle \sum_{i=1}^n w_i ( \overrightarrow{x_i} - )^2$$

K-means++算法

K-means$\Vert$算法

Canopy算法

Mini Batch K-means算法

K-means和Mini Batch K-means算法比较案例

聚类算法的衡量指标

• 混淆矩阵
• 均一性
• 完整性
• V-measure
• 调整兰德系数(ARI)
• 调整互信息(AMI)
• 轮廓系数(Silhouette)

均一性

• 均一性: 一个簇中只包含一个类别的样本, 则满足均一性; 其实也可以认为是正确率(每个聚簇中正确分类的样本数占该聚簇总样本书的比例和) $$p = \frac{1}{k} \displaystyle \sum_{i=1}^{k} \frac{N(C_i == K_i)}{N(K_i)}$$ N表示数量, $C_i$表示实际的类别, $K_i$表示在簇中间的类别, 总共k个簇

完整性

• 完整性: 同类别样本被归类到相同簇中, 则满足完整性; 每个聚簇中正确分类的样本数占该类型的总样本比例的和, 和之前讲的”召回率”有点类似
  $r = \frac{1}{k} \displaystyle \sum_{i=1}^{k} \frac{N(C_i == K_i)}{N(C_i)}$ - V-measure: 均一性和完整性的加权平均

V-measure

$$v_\beta = \frac{(1 + \beta^2) \cdot pr}{\beta^2 \cdot p + r}$$

轮廓系数

• 簇内不相似度
• 簇间不相似度
• 轮廓系数

层次聚类方法

凝聚的层次聚类AGNES算法

分裂的层次聚类DIANA算法

AGNES和DIANA算法优缺点

AGNES算法中簇间距离

层次聚类优化算法

BIRCH算法

CURE算法

BRICH算法案例

密度聚类算法

密度聚类方法的指导思想是: 只要样本点的密度大于某个阈值, 则将样本添加到最近的簇中

这类算法可以客服基于距离的算法只能发现凸聚类的缺点, 可以发现任意形状的聚类, 而且对噪声数据不敏感

计算复杂度高, 计算量大
常用的算法有:

• DBSCAN
• 密度最大值算法

DBSCAN算法

密度最大值聚类算法(MDCA)

密度聚类算法案例

谱聚类

拉普拉斯矩阵变换

谱聚类应用场景及面临的问题

谱聚类应用案例

聚类综合案例

不同聚类算法在不同数据分布情况下的聚类效果

图片压缩

有约束的最优化问题

• 最优化问题一般是指对于某一个函数而言, 求解在其指定作用域上的全局最小值问题, 一般分为三种情况, 这三种方法求出来的解都有可能有局部最小值, 只有当函数是凸函数的时候, 才可以得到全局最小值
  • 无约束问题, 一般求解方式为梯度下降法, 牛顿法, 坐标轴下降法, $ \displaystyle \min \limits_{x}f(x)$
  • 等式约束条件, 求解方式为拉格朗日乘子法, $\displaystyle \min \limits_{x}f(x); s.t: h_k(x)=0, k=1,2,\cdots, p$
  • 不等式约束条件, 求解方式为KKT条件 $$\displaystyle \min \limits_{x}f(x), s.t: h_k(x)=0, k=1,2,\cdots, p, g_j(x) \le 0, j=1, 2, \cdots, q$$

拉格朗日乘子法

$$\displaystyle \min \limits_{x}f(x), s.t: h_i(x)=0, i=1,2,\cdots, p$$ $$\displaystyle \min \limits_{x}f(x) + \displaystyle \sum_{i=1}^{p} \alpha_i h_i(x); \quad \alpha_i \ne 0$$

对偶问题

在优化问题中, 目标函数f(x)存在多种形式, 如果目标函数和约束条件都为变量x的线性函数, 则称问题为线性规划; 如果目标函数为二次函数, 则称优化问题为二次规划; 如果目标函数或者约束条件为非线性函数, 则称最优化问题为非线性规划. 每个线性规划问题都有一个对偶问题

• 对偶问题的对偶是愿问题
• 无论原始问题是否是凸的, 对偶问题都是凸优化问题
• 对偶问题可以给出原始问题的一个下界
• 当满足一定条件的时候, 原始问题和对偶问题的解是完美等价的

KKT条件

KKT条件是泛拉格朗日乘子法的一种形式, 主要应用在当我们的优化函数存在不等值约束的情况下的一种最优化解决方式; KKT条件即满足不等值约束的条件

$$\displaystyle \min \limits_{x}f(x); \quad s.t.: h_k(x)=0, k=1,2,\cdots,p; \quad g_j(x) \le 0, j=1, 2, \cdots, q$$ $$L(x, \alpha, \beta) = f(x) + \sum_{i=1}^{p}\alpha_ih_i(x) + \sum_{i=1}^{q}\beta_ig_i(x);\quad\alpha_i \ne 0, \beta_i \ge 0$$ $$\min \limits_{x}L(x, \alpha, \beta)$$

考虑简化的形式

$$\displaystyle \min \limits_{x}f(x); \quad s.t.: g_j(x) \le 0, j=1, 2, \cdots, q$$ $$L(x, \beta) = f(x) + \sum_{i=1}^{q}\beta_ig_i(x);\quad \beta_i \ge 0$$

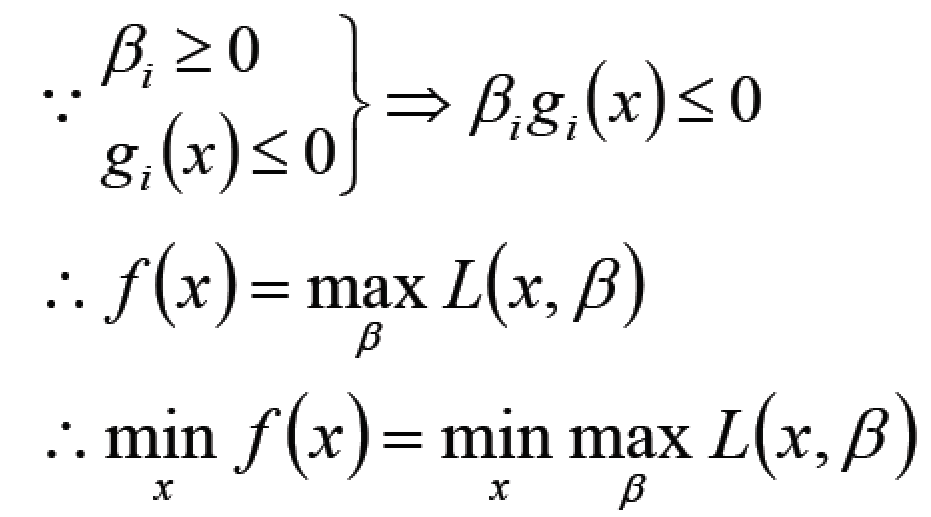
从上式可以看到, $\beta_i g_i(x) \le 0$, 那么它的最大值顶多是0, 那么$f(x) = L(x, \beta) - \displaystyle \sum_{i=1}^q{\beta_ig_i(x)}$, 由此可以得到$L(x, \beta)$的最大值顶多就是$f(x)$, 所以最后如果要求解$f(x)$的最小值, 即可以求解$\displaystyle \max \limits_{\beta}L(x, \beta)$的最小值

KKT条件总结

• 拉格朗日取得可行解的充要条件, $\nabla_xL(x, \alpha, \beta) = 0$
• 将不等式约束转换后的一个约束, 称为松弛互补条件, $\beta_ig_i(x) = 0, \quad i=1,2,\cdots,q$
• 初始约束条件, $h_i(x)=0, \quad i=1,2,\cdots,p$
• 初始约束条件, $g_i(x)\le0,\quad i=1,2,\cdots,q$
• 不等式约束需要满足的条件, $\beta_i\ge0,\quad i=1,2,\cdots,q$

参考拉格朗日乘子法和KKT条件

感知器模型

感知器模型的前提是数据线性可分

对于m个样本, 每个样本n维特征以及一个二元类别输出y, 如下:

$$\lbrace (x_1^{(1)}, x_2^{(1)}, \cdots, x_n^{(1)}), (x_1^{(2)}, x_2^{(2)}, \cdots, x_n^{(2)}), \cdots, (x_1^{(m)}, x_2^{(m)}, \cdots, x_n^{(m)}) \rbrace$$

目标是找到一个超平面, 即

$$\theta_0 + \theta_1x_1 + \cdots + \theta_nx_n = 0 \Rightarrow \theta x = 0$$

让一个类别的数据满足$\theta x > 0$, 另外一个类别满足$\theta x < 0$
感知器模型, $y=sign(\theta x )\begin{cases}
+1, \theta x > 0\\
-1, \theta x < 0\\
\end{cases}$

定义正确分类为: $y\theta x>0$, 定义错误分类为: $y\theta x<0$, 所以定义的损失函数为: 期望使分类错误的所有样本(m条样本)到超平面的距离之和最小

$$L = \displaystyle \sum_{i=1}^{m} \frac{-y^{(i)}\theta x^{(i)}}{\Vert \theta \Vert_2}$$

分子分母简化后

$$L = \displaystyle - \sum_{i=1}^{m} y^{(i)}\theta x^{(i)}$$

直接使用梯度下降法对损失函数进行求解, 由于m是分类错误对样本集合, 不是固定的, 所以我们不能使用批量梯度下降法(BGD)求解, 只能使用随机梯度下降(SGD)和小批量梯度下降法(MBGD), 一般使用SGD求解

$$\frac{\partial L(\theta)}{\partial \theta} = - \sum_{i=1}^{m} y^{(i)}\theta x^{(i)}$$ $$\theta^{k+1} = \theta^k + \alpha y^{(i)}x^{(i)}$$

SVM

• 梯度下降法, 拉格朗日乘子法, KKT条件回顾
• 感知器模型
• SVM线性可分
• SVM线性不可分
• 核函数
• SMO

线性可分SVM

在感知器模型中, 是可以找到多个可以分类的超平面将数据分开. 并且希望所有的点都离超平面尽可能的远, 但是实际上离超平面足够远的点基本上都是被正确分类的, 所以这个是没有意义的. 反而是离超平面很近的点, 这些点比较容易分错. 所以只要让离超平面比较近的点尽可能的远离这个超平面, 这样模型分类效果就会不错, 此即为SVM的思想.

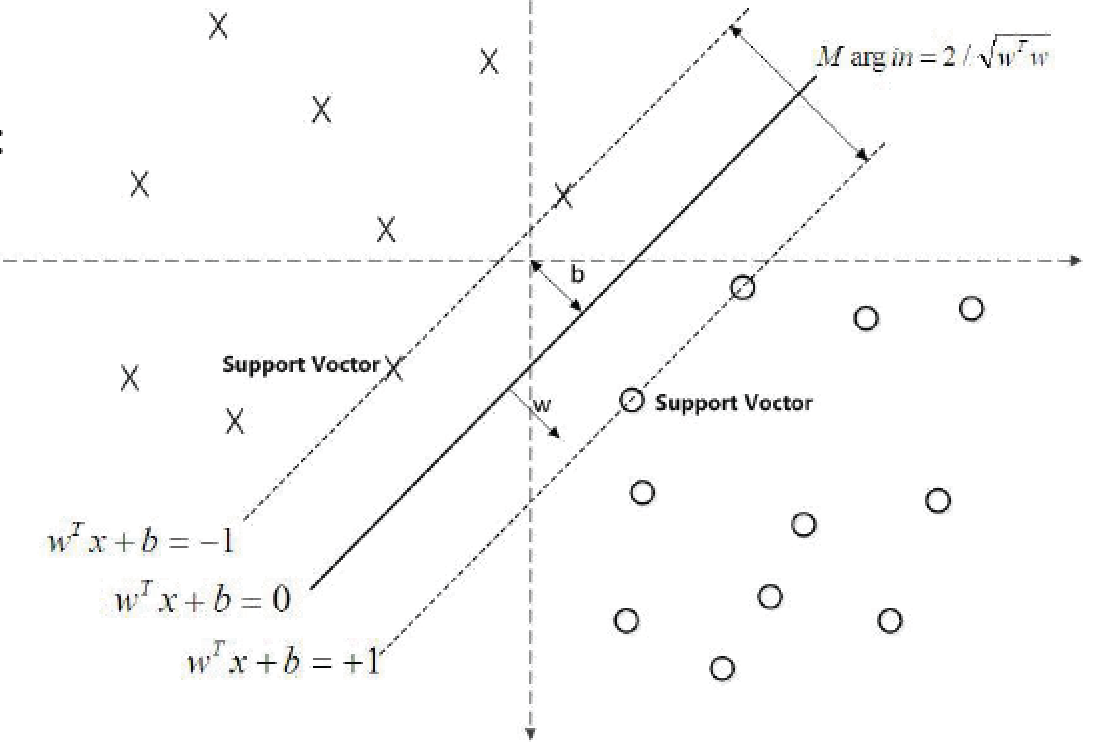
• 支持向量到超平面的距离为: $$\because w^T x + b = \pm 1$$ $$\because y \in \{+1, -1\}$$ $$\therefore \displaystyle \frac{y(w^Tx+b)}{\Vert w \Vert_2} = \frac{1}{\Vert w \Vert_2}$$

在SVM中支持向量到超平面的函数距离一般设置为1

SVM模型是让所有的分类点在各自类别的支持向量的两边(见公式(2)), 同时要求支持向量尽可能的远离这个超平面(见公式(1)), 用数学公式表示如下:

$$\max \limits_{w, b} \displaystyle \frac{1}{\Vert w \Vert_2} \tag{1}$$ $$s.t: y^{(i)}(w^Tx^{(i)}+b) \ge 1, \quad i=1, 2, \cdots, m \tag{2}$$ $$\because w^T = (w_1, w_2, \cdots, w_n)$$ $$\therefore \Vert w \Vert_2 = \sqrt{w_1^2 + w_2^2 + \cdots + w_n^2}$$

优化问题等价于$ \min \limits_{w, b} \Vert w \Vert_2; \quad s.t: y^{(i)}(w^Tx^{(i)}+b) \ge 1, \quad i=1, 2, \cdots, m$
那么SVM的目标函数/损失函数为:

$$J(w) = \displaystyle \frac{1}{2} \Vert w \Vert_2^2; \quad s.t: y^{(i)}(w^Tx^{(i)}+b) \ge 1, \quad i=1, 2, \cdots, m$$

优化目标为$w^{\ast}, b^{\ast} = \min \limits_{w, b} J(w)$
这时可以将此此时的目标函数和约束条件使用KKT条件转换为拉格朗日函数, 从而转化为无约束优化函数:

$$J(w) = \displaystyle \frac{1}{2} \Vert w \Vert_2^2; \quad s.t: 1 - y^{(i)}(w^Tx^{(i)}+b) \le 0, \quad i=1, 2, \cdots, m$$ $$L(w, b, \beta) = \displaystyle \frac{1}{2} \Vert w \Vert_2^2 + \sum_{i=1}^m \beta_i[1 - y^{(i)}(w^Tx^{(i)} + b)], \quad \beta_i \ge 0$$

引入拉格朗日乘子之后, 优化目标变成了:

$$\min \limits_{w, b} \max \limits_{\beta \ge 0} L(w, b, \beta)$$

根据拉格朗日对欧化特性, 将优化目标转换为等价的对偶问题

$$\max \limits_{\beta \ge 0} \min \limits_{w, b} L(w, b, \beta)$$

对于该优化函数, 要先求优化函数对于w和b的极小值, 然后再求解对于拉格朗日乘子$\beta$的极大值

优化函数L对于w和b的极小值, 可以通过对函数L分别对w和b求偏导数得到

$$\displaystyle \frac{\partial L}{\partial w} = 0 \Rightarrow w = \sum_{i=1}^{m} \beta_i y^{(i)} x^{(i)}$$ $$\displaystyle \frac{\partial L}{\partial b} = 0 \Rightarrow \sum_{i=1}^{m} \beta_i y^{(i)} = 0$$

将求解出的w和b带入优化函数L中, 那么优化后的函数如下:

$$\begin{align} \mathcal{l}(\beta) &= \displaystyle \frac{1}{2} \Vert w \Vert_2^2 + \sum_{i=1}^{m} \beta_i [1 - y^{(i)}(w^Tx^{(i)} + b)]\\ &= \frac{1}{2} w^T w - \sum_{i=1}^{m} \beta_i y^{(i)} w^T x^{(i)} - \sum_{i=1}^{m} \beta_i y^{(i)} b + \sum_{i=1}^{m} \beta_i\\ &= \frac{1}{2} w^T \sum_{i=1}^{m} \beta_i y^{(i)} x^{(i)} - \sum_{i=1}^{m} \beta_i y^{(i)} w^T x^{(i)} - \sum_{i=1}^{m} \beta_i y^{(i)} b + \sum_{i=1}^{m} \beta_i\\ &= - \frac{1}{2} w^T \sum_{i=1}^{m} \beta_i y^{(i)} x^{(i)} - b \sum_{i=1}^{m} \beta_i y^{(i)} + \sum_{i=1}^{m} \beta_i \\ &= - \frac{1}{2} w^T \sum_{i=1}^{m} \beta_i y^{(i)} x^{(i)} + \sum_{i=1}^{m} \beta_i \\ &= - \frac{1}{2} (\sum_{i=1}^{m} \beta_i y^{(i)} x^{(i)})^T (\sum_{i=1}^{m} \beta_i y^{(i)} x^{(i)}) + \sum_{i=1}^{m} \beta_i \\ &= - \frac{1}{2} (\sum_{i=1}^{m} \beta_i y^{(i)} {(x^{(i)})}^T) (\sum_{i=1}^{m} \beta_i y^{(i)} x^{(i)}) + \sum_{i=1}^{m} \beta_i \\ &= - \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \beta_i \beta_j y^{(i)} y^{(j)} {x^{(i)}}^T x^{(j)} + \sum_{i=1}^{m} \beta_i \\ \end{align}$$ $$\therefore l(\beta) = - \frac{1}{2} \sum_{i=1, j=1}^{m} \beta_i \beta_j y^{(i)} y^{(j)} {x^{(i)}}^T x^{(j)} + \sum_{i=1}^{m} \beta_i; \quad s.t: \sum_{i=1}^{m} \beta_i y^{(i)} = 0, \quad \beta_i \ge 0, \quad i=1, 2, \cdots, m$$

此时得到的优化函数只和$\beta$有关, 这时直接最大化优化函数得到$\beta$值, 从而最终得到w和b的值

$$\max \limits_{\beta \ge 0} l(\beta); \quad s.t: \sum_{i=1}^{m} \beta_i y^{(i)} = 0$$

该优化问题等价于:

$$\min \limits_{\beta \ge 0} - l(\beta); \quad s.t: \sum_{i=1}^{m} \beta_i y^{(i)} = 0$$

即:

$$\min \limits_{\beta_i \ge 0} l(\beta) = \min \limits_{\beta_i \ge 0} \frac{1}{2} ( \sum_{i=1, j=1}^{m} \beta_i \beta_j y^{(i)} y^{(j)} {x^{(i)}}^T x^{(j)} - \sum_{i=1}^{m} \beta_i); \quad s.t: \sum_{i=1}^{m} \beta_i y^{(i)} = 0$$

$\beta$值的求解采用SMO算法

假设求解得到的$\beta$值为$\beta^{\ast}$, 则根据w, b, $\beta$的关系, 分别计算如下:

$$w^{\ast} = \displaystyle \sum_{i=1}^{m} \beta_i^{\ast} y^{(i)} x^{(i)}$$

b的计算采用所有支持向量的计算均值

$$\because y^s (w^T x^s +b) = y^s (\displaystyle \sum_{i=1}^{m} \beta_i^{\ast} y^{(i)} {x^{(i)}}^T x^s + b ) = 1$$ $$\therefore b^{\ast} = \frac{1}{y^s} - \sum_{i=1}^{m} \beta_i^{\ast} y^{(i)} {x^{(i)}}^T x^s$$ $$又\because y^s \in \{1, -1\}$$ $$\therefore b^{\ast} = {y^s} - \sum_{i=1}^{m} \beta_i^{\ast} y^{(i)} {x^{(i)}}^T x^s$$

在这里$(x^s, y^s)$是支持向量, 根据KKT条件中的对欧互补条件(松弛约束条件), 支持向量必须满足以下公式:

$$\beta_i (y^{(i)}(w^T x^{(i)} + b) - 1 ) = 0$$ $$\{ (x^{(i), y^{(i)}}) \quad | \quad \beta_i > 0, \quad i=1,2,\cdots,m \}$$

线性可分SVM算法流程

输入线性可分的m个样本数据$\{ (x^1, y^1), (x^2, y^2), \cdots, (x^m, y^m)\}$, 其中x为n维的特征向量, y为二元输出, 取值为$+1$或者$-1$, SVM输出为参数$w$, $b$以及分类决策函数.

• 构造约束优化维问题, $\displaystyle \min \limits_{\beta_i \ge 0} \frac{1}{2} ( \sum_{i=1, j=1}^{m} \beta_i \beta_j y^{(i)} y^{(j)} {x^{(i)}}^T x^{(j)} - \sum_{i=1}^{m} \beta_i); \quad s.t: \sum_{i=1}^{m} \beta_i y^{(i)} = 0 $
• 使用SMO算法求出上述优化中对应的最优解$\beta^{\ast}$
• 找出所有的支持向量集合$S = \{ (x^{(i)}, y^{(i)}) \quad | \quad \beta_i > 0, \quad i=1,2,\cdots,m \}$
• 更新参数$w^{\ast}$和$b^{\ast}$的值, $w^{\ast} = \displaystyle \sum_{i=1}^{m} \beta_i^{\ast} y^{(i)} x^{(i)}, \quad b^{\ast} = \frac{1}{s} \sum_{s=1}^{S} ({y^s} - \sum_{i=1}^{m} \beta_i^{\ast} y^{(i)} {x^{(i)}}^T x^s) $
• 构建最终的分类决策函数, $f(x)=sign(w^{\ast} \cdot x + b^{\ast})$

$$\beta_1 \beta_1 3*3*3*3 + \beta_1 \beta_2 3*3*3*4 - \beta_1 \beta_33*1*3*1 + \beta_2 \beta_1 3*3*4*3 + \beta_2 \beta_2 3*3*4*4 - \beta_2 \beta_3 3*1*4*1 - \beta_3 \beta_1 1*3*1*3 - \beta_3 \beta_2 1*3*4*1 - \beta_3 \beta_3 1*1*1*1$$ $$81\beta_1 \beta_1 + 216\beta_1 \beta_2 - 18\beta_1 \beta_3 + 144 \beta_2 \beta_2 - 24 \beta_2 \beta_3 + \beta_3 \beta_3$$

这里的例子没有理解

svm参考例子1

线性可分SVM总结

• 要求数据必须是线性可分的
• 纯线性可分的SVM模型对于异常数据的预测可能会不太准
• 对于线性可分的数据, SVM分类器的效果非常不错

SVM的软间隔模型

线性可分SVM中要求数据必须是线性可分的, 才可以找到分类的超平面, 但是有的时候线性数据集中存在少量的异常点, 由于这些异常点导致了数据集不能够线性可分; 正常数据是线性可分的, 但是由于存在异常点数据, 导致数据集不能够线性可分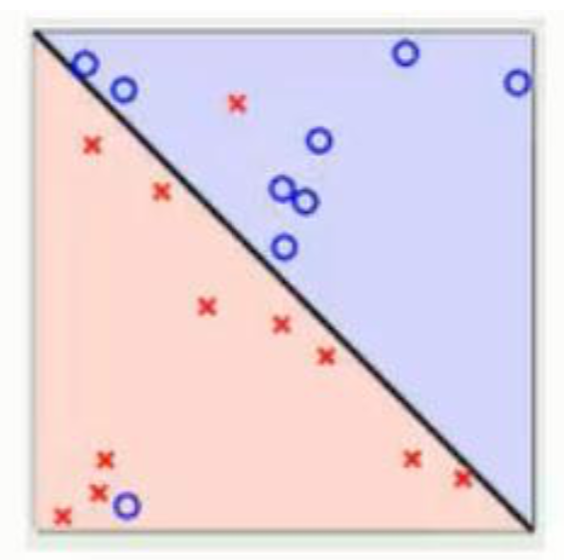

如果线性数据中存在异常点导致没法直接使用SVM线性分割模型的时候, 那我们可以通过引入软间隔的概念来解决这个问题

• 硬间隔: 认为线性可分SVM中的距离度量就是硬间隔, 在线性划分SVM中, 要求函数距离一定是大于1的, 最大化硬间隔条件为: $$\min \limits_{w,b} \frac{1}{2} \Vert w \Vert_{2}^{2}; \quad s.t: \quad y^{(i)}(w^Tx^{(i)} + b) \le 1, i=1,2,\cdots,m$$
• 软间隔: SVM对于训练集中的每个样本都引入一个松弛因子($\xi$), 使得函数距离加上松弛因子后的值是大于或者等于1; 这表示相对于硬间隔, 对样本到超平面距离的要求放松了 $$y^{(i)}(w^Tx^{(i)} + b) \ge 1 - \xi_i, i=1,2,\cdots,m, \quad \xi_i \ge 0$$

• 松弛因子($\xi$)越大, 表示样本点离超平面越近, 如果松弛因子大于1, 那么允许该样本点分错, 所以加入松弛因子是有成本的, 过大的松弛因子可能会导致模型分类错误, 所以最终的目标函数就转换成为:

  $$\min \limits_{w,b} \frac{1}{2} \Vert w \Vert_{2}^{2} + C \displaystyle \sum_{i=1}^{m} \xi_i$$ $$y^{(i)}(w^Tx^{(i)} + b) \ge 1 - \xi_i, \quad \xi_i \ge 0, \quad i=1,2,\cdots,m$$

  其中, 函数中的$C > 0$是惩罚系数, 是一个超参, 类似于L1/L2 norm中的参数; C越大表示对误分类的惩罚越大, C越小表示对误分类的惩罚越小; C值的给定需要调参

• 同线性可分SVM, 构造软间隔最大化的约束问题对应的拉格朗日函数如下:

  $$L(w,b,\xi,\beta,\mu) = \frac{1}{2} \Vert w \Vert_{2}^{2} + C \displaystyle \sum_{i=1}^{m}\xi_i + \displaystyle \sum_{i=1}^{m} \beta_i [1-\xi_i-y^{(i)}(w^Tx^{(i)}+b)]-\displaystyle \sum_{i=1}^{m}\mu_i \xi_i, \quad \beta_i \ge 0, \mu_i \ge 0$$

  从而可以将优化目标函数转换为:

  $$\min \limits_{w,b,\xi} \max \limits_{\beta, \mu} L(w, b, \xi, \beta, \mu)$$
• 优化条件同样满足KTT条件, 所有使用拉格朗日对偶将优化问题转换为等价的对偶问题 $$\max \limits_{\beta, \mu} \min \limits_{w,b,\xi} L(w, b, \xi, \beta, \mu)$$

先求优化函数对于$w,b,\xi$的极小值, 这个可以通过分别优化函数L求$w,b,\xi$的偏导数, 从而可以得到$w,b,\xi$关于$\beta$和$\mu$之间的关系

$$\frac{\partial L}{\partial w} = 0 \Rightarrow w - \sum_{i=1}^{m}\beta_iy^{(i)}x^{(i)} = 0 \Rightarrow w = \sum_{i=0}^{m}\beta_iy^{(i)}x^{(i)}$$ $$\frac{\partial L}{\partial b} = 0 \Rightarrow - \sum_{i=1}^{m}\beta_iy^{(i)} = 0 \Rightarrow \sum_{i=1}^{m}\beta_iy^{(i)} =0$$ $$\frac{\partial L}{\partial \xi_i} = 0 \Rightarrow C - \beta_i - \mu_i = 0$$

将$w,b,\xi$的值带入L函数中, 就可以消去优化函数中的$w,b,\xi$, 定义优化中后的函数如下:

$$l(\beta) = \sum_{i=1}^{m}\beta_i - \frac{1}{2}\sum_{i=1,j=1}^{m}\beta_i\beta_jy^{(i)}y^{(j)}x^{(i)^{T}}x^{(j)}; \quad s.t: \sum_{i=1}^{m}\beta_iy^{(i)}=0, C-\beta_i - \mu_i = 0, \beta_i \ge 0, i=1,2,\cdots,m, \mu_i \ge 0, i=1,2,\cdots,m$$

最终优化后的目标函数/损失函数和线性可分SVM模型基本一样, 除了约束条件不同而已, 也就是说也可以使用SMO算法来求解

$$\min\frac{1}{2}\sum_{i=1,j=1}^{m}\beta_i\beta_jy^{(i)}y^{(j)}x^{(i)^{T}}x^{(j)} - \sum_{i=1}^{m}\beta_i$$ $$s.t: \sum_{i=1}^{m}\beta_iy^{(i)}=0, 0 \le \beta_i \le C, i=1,2,\cdots,m$$

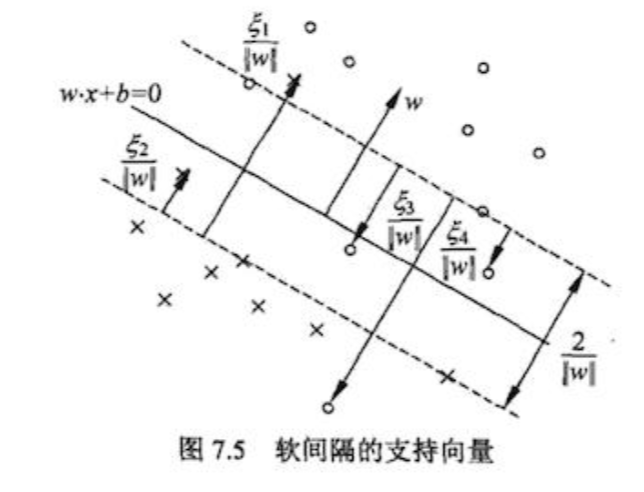
• 在硬间隔最大化的时候, 支持向量比较简单, 就是离超平面的函数距离为1的样本点就是支持向量
• 在软间隔中, 根据KKT条件中的对偶互补条件: $\beta(y(wx+b)-1+\xi)=0$, 从而有:
  • 当$0<\beta_i \le C$的时候, 并且$\xi_i=0$的样本点均是支持向量(即所有的$0<\beta_i < C$). 即满足$|wx+b|=1$的所有样本均是支持向量
  • 软间隔和硬间隔中的支持向量的规则是一样的
    

SVM软间隔模型算法流程

输入线性可分的m个样本数据${(x^1, y^1), (x^2, y^2), \cdots, (x^m, y^m)}$, 其中x为n维的特征向量, y为二元输出, 取值为+1或者-1； SVM模型输出为参数$w,b$以及分类决策函数

• 选择一个惩罚系数C>0, 构造约束优化问题, $\displaystyle \min \limits_{\beta_i \ge 0} \frac{1}{2} ( \sum_{i=1, j=1}^{m} \beta_i \beta_j y^{(i)} y^{(j)} {x^{(i)}}^T x^{(j)} - \sum_{i=1}^{m} \beta_i); \quad s.t: \sum_{i=1}^{m} \beta_i y^{(i)} = 0, 0 \le \beta_i \le C, i=1,2,\cdots,m$
• 使用SMO算法求出上述优化中对应的最优解$\beta^*$
• 找出所有的支持向量集合$S = \{ (x^{(i)}, y^{(i)}) \quad | \quad 0 < \beta_i \le C, \xi_i = 0, i = 1, 2, \cdots, m $
• 更新参数$w^{\ast}$和$b^{\ast}$的值, $w^{\ast} = \displaystyle \sum_{i=1}^{m} \beta_i^{\ast} y^{(i)} x^{(i)}, \quad b^{\ast} = \frac{1}{s} \sum_{s=1}^{S} ({y^s} - \sum_{i=1}^{m} \beta_i^{\ast} y^{(i)} {x^{(i)}}^T x^s) $
• 构建最终的分类器$f(x)=sign(w^{\ast} x + b^{\ast})$

SVM软间隔模型总结

• 可以解决线性数据中携带异常点的分类模型构建的问题
• 通过引入惩罚系数(松弛因子), 可以增加模型的泛化能力, 即鲁棒性
• 如果给定的惩罚系数越小, 表示在模型构建的时候, 就允许存在越多的分类错误的样本, 表示此时模型的准确率会比较低; 如果惩罚系数越大, 表示模型在构建的时候, 就越不允许存在分类错误的样本, 表示此时模型的准确率会比较高