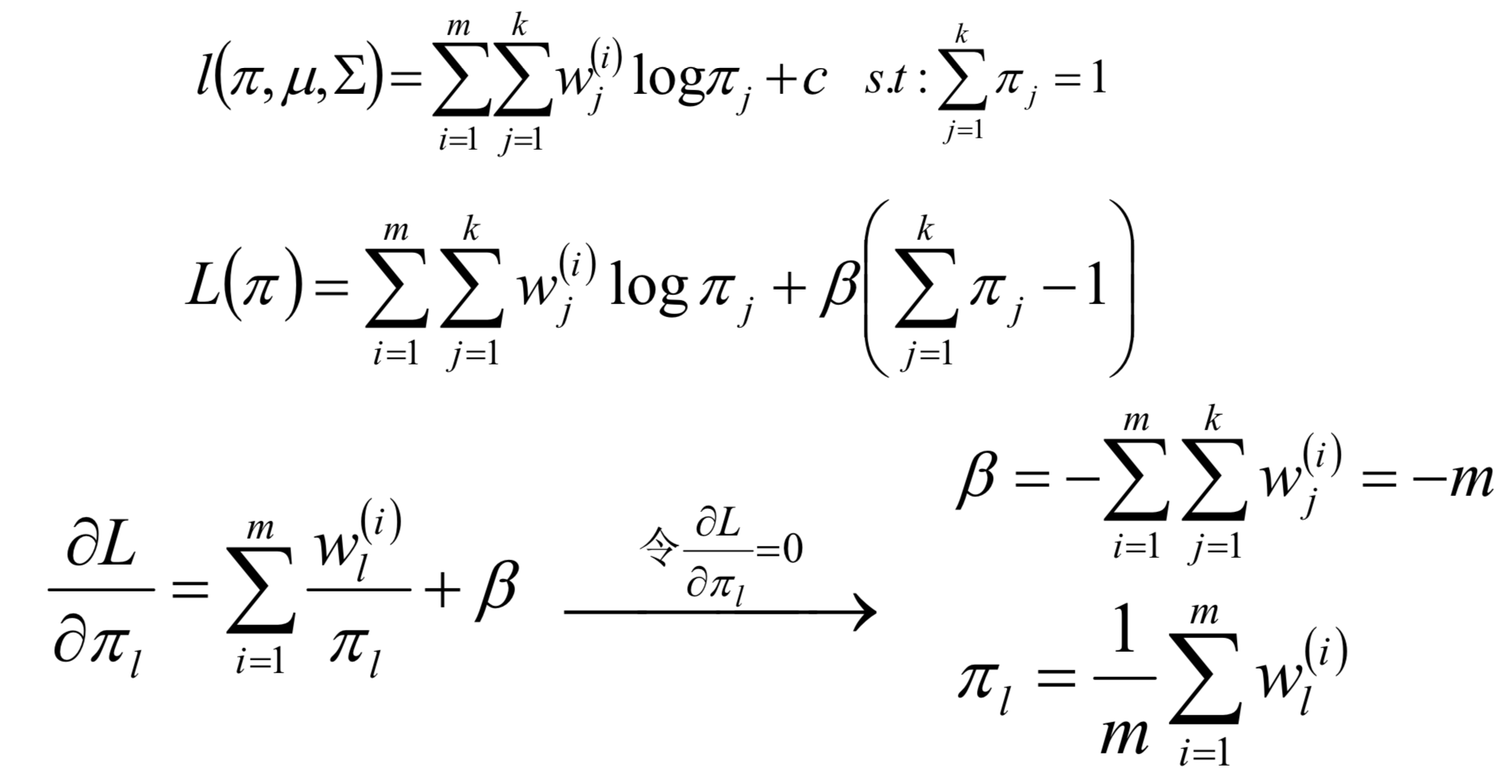L8

多项式回归

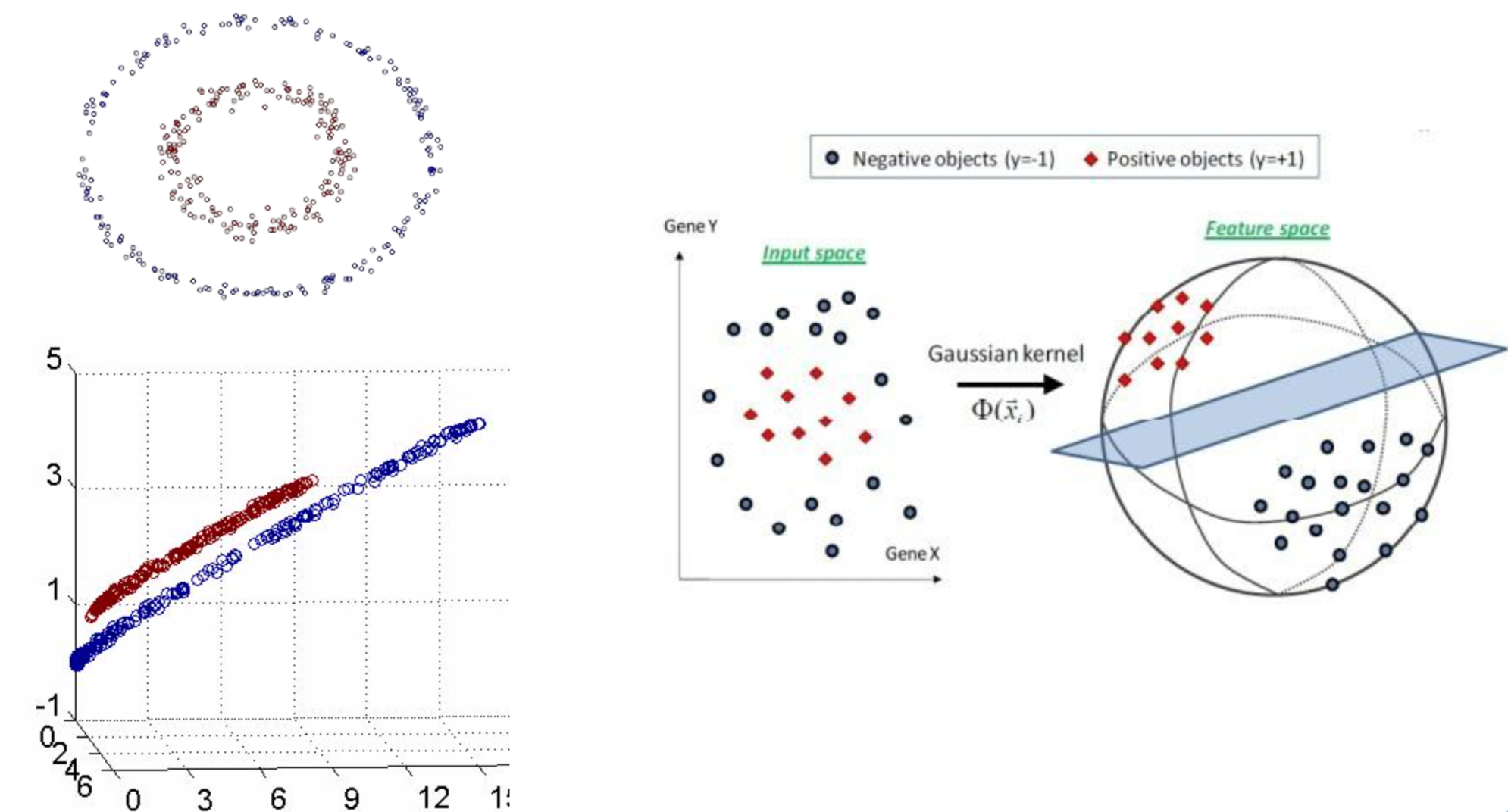
在线性回归中, 可以通过多项式扩展将低维度扩展成为高维度数据, 从而可以使用线性回归模型来解决问题. 即对于二维空间中不是线性可分的数据, 将其映射到高维空间中后, 变成了线性可分的数据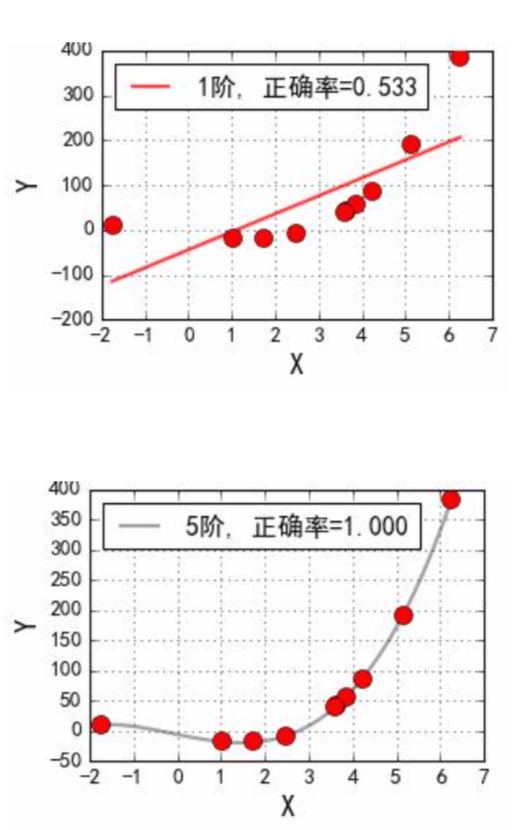

两维线性模型:

$$h_\theta(x_1, x_2) = \theta_0 + \theta_1 x_1 + \theta_2 x_2$$ $$(x_1, x_2) \quad \underrightarrow{多项式扩展} \quad (x_1, x_2, x_1^2, x_2^2, x_1x_2)$$

五维线性模型:

$$h_\theta(x_1, x_2) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3 + \theta_4 x_4 + \theta_5 x_5$$ $$\underrightarrow{等价于} \quad h_\theta(x_1, x_2) = \theta_0 + \theta_1 z_1 + \theta_2 z_2 + \theta_3 z_3 + \theta_4 z_4 + \theta_5 z_5$$

核函数

假设函数$\phi$是一个从低维特征空间到高维特征空间到一个映射, 那么如果存在函数$K(x,z)$, 对于任意的低维度特征向量x和z, 都有$K(x, z) = \phi(x) \cdot \phi(z)$, 该函数称为核函数

核函数在解决线性不可分问题的时候, 采用的方式是: 使用低维特征空间的计算来避免在高维特征空间中向量内积的恐怖计算量, 也就是说此时SVM模型可以应用在高维特征空间中数据可线性分割的优点, 同时也避免来引入这个高维特征空间恐怖的内积计算量

设两个向量$x_1 = (\mu_1, \mu_2)^T$和$x_2 = (\eta_1, \eta_2)^T$, 映射过后的内积为:

$$\phi(x_1) \cdot \phi(x_2) = \mu_1 \eta_1 + \mu_2 \eta_2 + \mu_1^2 \eta_1^2 + \mu_2^2 \eta_2^2 + \mu_1 \mu_2 \eta_1 \eta_2$$

同时发现另外一个公式:

$$(x_1 \cdot x_2 + 1)^2 = 2\mu_1 \eta_1 + 2\mu_2 \eta_2 + \mu_1^2 \eta_1^2 + \mu_2^2 \eta_2^2 + 2\mu_1 \mu_2 \eta_1 \eta_2 + 1$$

上述两个公式非常相似, 只要乘上一个相关系数, 就可以让两个式子的值相等, 这样就可以将五维空间的一个内积转换为两维的内积运算

• 线性核函数(Linear Kernel) $$K(x, z) = x \cdot z$$
• 多项式核函数(polynomial Kernal), 其中$\gamma, r, d$属于超参, 需要调参定义 $$K(x, z) = (\gamma x \cdot r)^d$$
• 高斯核函数(Gaussian Kernal), 其中$\gamma$属于超参, 要求大于0, 需要调参定义 $$K(x,z) = e^{-\gamma \Vert x-z \Vert_{2}^{2}}$$
• Sigmoid核函数(Sigmoid Kernal), 其中$\gamma, r$属于超参, 需要调参定义 $$K(x,z) = tanh(\gamma x \cdot z + r)$$

核函数总结

• 核函数可以自定义, 核函数必须是正定核函数, 即Gram矩阵是半正定矩阵
• 核函数的价值在于它虽然也是将特征进行从低维度到高维度的转换, 但核函数事先在低维上进行计算, 而将实质的分类效果表现在了高维上, 也就避免了直接在高维空间上的复杂计算
• 通过核函数, 可以将非线性可分的数据转换为线性可分数据

\begin{bmatrix}
{K(x_1, x_1)}&{K(x_1, x_2)}&{\cdots}&{K(x_1, x_m)}\\
{K(x_2, x_1)}&{K(x_2, x_2)}&{\cdots}&{K(x_2, x_m)}\\
{\vdots}&{\vdots}&{\ddots}&{\vdots}\\
{K(x_m, x_1)}&{K(x_m, x_2)}&{\cdots}&{K(x_m, x_m)}\\
\end{bmatrix}

高斯核函数

令$z=x$, 进行多维变换后, 应该是同一个向量, 从而得到以下公式:

$$\begin{align} K(x, z) &= e^{-\gamma \Vert x-z \Vert_2^2} \\ &= e^{-\gamma \Vert x \Vert_2^2} \cdot e^{-\gamma \Vert z \Vert_2^2} \cdot e^{2\gamma x \cdot z} \\ & \overset{\text{泰勒展开}}{=} e^{-\gamma \Vert x \Vert_2^2} \cdot e^{-\gamma \Vert z \Vert_2^2} (\displaystyle \sum_{i=0}^{+\infty} \frac{(2\gamma x \cdot z)^i}{i!}) \\ &= \displaystyle \sum_{i=0}^{+\infty} e^{-\gamma \Vert x \Vert_2^2} \cdot e^{-\gamma \Vert z \Vert_2^2} \frac{(2\gamma x \cdot z)^i}{i!} & \Rightarrow \phi(x) = e^{-\gamma \Vert x \Vert_2^2} \cdot (1, \sqrt{\frac{(2 \gamma)^1}{1!}} \Vert x\Vert_2^1, \sqrt{\frac{(2 \gamma)^2}{2!}} \Vert x\Vert_2^2, \cdots) \\ & = \displaystyle \sum_{i=0}^{+\infty} e^{-\gamma \Vert x \Vert_2^2} \cdot e^{-\gamma \Vert z \Vert_2^2} \sqrt{\frac{(2\gamma)^i}{i!}} \sqrt{\frac{(2\gamma)^i}{i!}} \Vert x \Vert_2^i \Vert z \Vert_2^i \\ &= \phi(x) \cdot \phi(z)\\ \end{align}$$

非线性可分SVM

不管是线性可分SVM还是加入惩罚系数的软间隔线性可分SVM其实都是要求数据本身都是线性可分的, 对于完全不可以线性可分的数据, 这两种算法模型就没法解决这个问题了

SMO

未完待续

贝叶斯算法

贝叶斯定理相关公式

朴素贝叶斯算法

朴素贝叶斯算法推导

朴素贝叶斯算法流程

高斯朴素贝叶斯

伯努利朴素贝叶斯

多项式朴素贝叶斯

案例一: 鸢尾花数据分类

案例二: 文本数据分类

贝叶斯网络

最简单的贝叶斯网络

全连接贝叶斯网络

正常贝叶斯网络

实际贝叶斯网络: 判断是否下雨

贝叶斯网络判定条件独立

如果x是连续的, 一般选择高斯朴素贝叶斯; 如果x是离散的, 一般选择多项式朴素贝叶斯; 如果x既有连续值又有离散值, 选择高斯朴素贝叶斯

EM

最大似然估计回顾

MLE就是利用已知的样本结果, 反推最有可能(最大概率)导致这样结果的参数值的计算过程. 就是给定了一定的数据, 假定知道数据是从某种分布中随机抽取出来的, 但是不知道这个分布具体的参数值, 即”模型已定, 参数未知”, MLE就是用来估计模型的参数的. MLE的目标是找出一组参数(模型中的参数), 使得模型产出观察数据的概率最大.

$$\displaystyle arg\max \limits_{\theta}p(X;\theta)$$

贝叶斯算法估计

• 贝叶斯算法估计是一种从先验概率和样本分布情况来计算后验概率的一种方式
• 贝叶斯算法中的常见概念
  • p(A)是事件A的先验概率或者边缘概率
  • p(A|B)是已知B发生后A发生的条件概率, 也称为A的后验概率
  • p(B|A)是已知A发生后B发生的条件概率, 也称为B的后验概率
  • p(B)是事件B的先验概率或者边缘概率 $$p(AB) = p(A)p(B|A) = p(B)p(A|B) \Rightarrow p(A|B) = \frac{p(A)p(B|A)}{p(B)}$$ $$p(A_i|B) = \frac{p(A_i)p(B|A_i)}{p(B)} = \frac{p(A_i)p(B|A_i)}{\displaystyle \sum_j p(B|A_j)p(A_j)}$$ $$f(\theta|x) = \frac{f(x|\theta)g(\theta)}{\displaystyle \int_{\theta^{'} \in \Theta}f(x|{\theta}^{'})g(\theta^{'})}$$

假设有5个盒子, 假定每个盒子中都有黑白两种球, 并且黑白球的比例如下; 已知从这5个盒子中的任意一个盒子中有放回的抽取两个球, 且均为白球, 问这两个球是从哪个盒子中抽取出来的?

盒子编号	白球(p)	黑球(q)
1	0	1
2	0.3	0.7
3	0.5	0.5
4	0.7	0.3
5	1	0

	1	2	3	4	5
p(A)	0.2	0.2	0.2	0.2	0.2

使用MLE(最大似然估计), 结论是从第5个盒子抽取的球:

$$L(X;p) = p^2 \quad \underrightarrow{arg\max L(X;p)} \quad p=1$$

使用贝叶斯算法估计, 结论是从第5个盒子抽取的球: 假设抽出白球为事件B, 从第i个盒子中抽取为事件$A_i$

$p(B|A_i)$, 抽到第i个盒子的概率 乘以 在第i个盒子中第一次抽出的球为白球的概率 乘以 在第i个盒子中第二次抽出的球为白球的概率

$$p(B|A_1) = 0.2 * 0 * 0 = 0$$ $$p(B|A_2) = 0.2 * 0.3 * 0.3 = 0.018$$ $$p(B|A_3) = 0.2 * 0.5 * 0.5 = 0.05$$ $$p(B|A_4) = 0.2 * 0.7 * 0.7 = 0.098$$ $$p(B|A_5) = 0.2 * 1 * 1 = 0.2$$

$p(B)$, 从任意一个盒子中有放回的抽取两个球, 且均为白球的概率

$$p(B) = \sum_{i=1}^{5} p(B|A_i) = 0 + 0.018 + 0.05 + 0.098 + 0.2 = 0.366$$

$p(A_1|B)$, 两抽为白的是第一个盒子的后验概率
$p(A_1)$, 抽到第一个盒子的先验概率
$p(B|A_1)$, 抽到第一个盒子并且两抽为白的条件概率
$p(B)$, 任意的盒子, 两抽为白的边缘概率

$$p(A_1|B) = \frac{p(A_1)p(B|A_1)}{p(B)} = \frac{0.2 * 0}{0.366} = 0$$ $$p(A_2|B) = \frac{p(A_2)p(B|A_2)}{p(B)} = \frac{0.2 * 0.018}{0.366} = 0.2 * 0.049$$ $$p(A_3|B) = \frac{p(A_3)p(B|A_3)}{p(B)} = \frac{0.2 * 0.05}{0.366} = 0.2 * 0.137$$ $$p(A_4|B) = \frac{p(A_4)p(B|A_3)}{p(B)} = \frac{0.2 * 0.098}{0.366} = 0.2 * 0.268$$ $$p(A_5|B) = \frac{p(A_5)p(B|A_3)}{p(B)} = \frac{0.2 * 0.2}{0.366} = 0.2 * 0.546$$

现在不是从5个盒子中任选一个盒子进行抽取, 而是按照一定的概率选择对应的盒子, 概率如下. 结论是从第4个盒子抽取的

	1	2	3	4	5
p(A)	0.1	0.2	0.2	0.4	0.1

$$p(A_1|B) = \frac{p(A_1)p(B|A_1)}{p(B)} = \frac{0.1 * 0}{0.366} = 0$$ $$p(A_2|B) = \frac{p(A_2)p(B|A_2)}{p(B)} = \frac{0.2 * 0.018}{0.366} = 0.2 * 0.049$$ $$p(A_3|B) = \frac{p(A_3)p(B|A_3)}{p(B)} = \frac{0.2 * 0.05}{0.366} = 0.2 * 0.137$$ $$p(A_4|B) = \frac{p(A_4)p(B|A_3)}{p(B)} = \frac{0.4 * 0.098}{0.366} = 0.2 * 0.536$$ $$p(A_5|B) = \frac{p(A_5)p(B|A_3)}{p(B)} = \frac{0.1 * 0.2}{0.366} = 0.2 * 0.366$$

最大后验概率估计

MAp(Maximum a posteriori estimation), 和MLE一样, 都是通过样本估计参数$\theta$的值; 在MLE中, 是使得似然函数$p(X|\theta)$最大的时候参数$\theta$的值, MLE中假设先验概率是一个等值的; 而在MAp中, 则是求$\theta$使$p(X|\theta)p(\theta)$的值最大, 这就要求$\theta$值不仅仅是让似然函数最大, 同时要求$\theta$本身出现的先验概率也得比较大

可以认为MAp是贝叶斯算法的一种应用

$$p(\theta^{'}|X) = \frac{p(\theta^{'})p(X|\theta^{'})}{p(X)} \quad \rightarrow \quad arg\max \limits_{\theta^{'}} p(\theta^{'}|X) \quad \rightarrow \quad arg\max \limits_{\theta^{'}} p(\theta^{'})p(X|\theta^{'})$$

K-means算法回顾

K-means算法, 也叫做k-均值聚类算法, 是一种非常广泛使用的聚类算法之一
假定输入样本为$S=x_1, x_2, \cdots, x_m$, 则算法步骤为:

• 选择初始的k个簇中心点$\mu_1, \mu_2, \cdots, \mu_k$
• 将样本$x_i$标记为距离簇中心最近的簇: $label_i = arg \min \limits_{1 \le j \le k} \Vert x_i - \mu_j \Vert$
• 迭代处理所有样本数据, 计算出各个样本点所属的对应簇
• 更新簇中心点坐标$\mu_i = \displaystyle \frac{1}{\vert C_i \vert} \sum_{j \in C_i} x_j$
• 重复上述三个操作, 直到算法收敛
  算法收敛条件: 迭代次数/簇中心变化率/MSE/MAE $$J(k, \mu) = \frac{1}{m}\sum_{i=1}^{m}\Vert x^{(i)} - \mu_{k^{(i)}} \Vert^2$$ $$k, \mu = arg \min \limits_{k, \mu} J(k, \mu)$$

EM算法引入

公司有男同事=[A，B，C]，同时有很多漂亮的女职员=[小甲，小章，小乙]。（请勿对号入座）你迫切的怀疑这些男同事跟这些女职员有“问题”。为了科学的验证你的猜想，你进行了细致的观察。于是：
观察数据:

• A，小甲、小乙一起出门了；
• B，小甲、小章一起出门了；
• B，小章、小乙一起出门了；
• C，小乙一起出门了；

初始化

你觉得三个同事一样帅，一样有钱，三个美女一样漂亮，每个人都可能跟每个人有关系。所以，每个男同事跟每个女职员“有问题”的概率都是1/3;

EM算法中的E步骤

• A和小甲出去过的次数为$\displaystyle \frac{1}{2} \cdot \frac{1}{3} = \frac{1}{6}$, 和小乙出去的次数也是$\displaystyle \frac{1}{6}$
• B和小甲, 小章出去的次数分别为$\displaystyle \frac{1}{6}$
• B和小章, 小乙出去的次数分别为$\displaystyle \frac{1}{6}$
• C和小乙出去的次数为$\displaystyle \frac{1}{3}$

归纳总结:

• A和小甲出去了$\displaystyle \frac{1}{6}$次, 和小乙出去了$\displaystyle \frac{1}{6}$次
• B和小甲出去了$\displaystyle \frac{1}{6}$次, 和小乙出去了$\displaystyle \frac{1}{6}$次, 和小章出去了$\displaystyle \frac{1}{3}$次
• C和小乙出去了$\displaystyle \frac{1}{3}$次

EM算法中的M步骤

• A和小甲, 小乙有问题的概率为$\displaystyle \frac{1/6}{1/6 + 1/6} = \frac{1}{2}$
• B和小甲, 小乙有问题的概率为$\displaystyle \frac{1/6}{1/6 + 1/6 + 1/6 + 1/6} = \frac{1}{4}$
• B和小章有问题的概率为$\displaystyle \frac{1/3}{1/6 + 1/6 + 1/3} = \frac{1}{2}$
• C和小乙有问题的概率为$\displaystyle \frac{1/3}{1/3} = 1$

第二次迭代EM算法中的E步骤

根据已知条件

• A，小甲、小乙一起出门了；
• B，小甲、小章一起出门了；
• B，小章、小乙一起出门了；
• C，小乙一起出门了；

结合上个M步骤更新的概率

• A和小甲出去了$\displaystyle \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}$次, 和小乙出去了$\displaystyle \frac{1}{4}$次
• B和小甲出去了$\displaystyle \frac{1}{2} \cdot \frac{1}{4} = \frac{1}{8}$次, 和小章出去了$\displaystyle \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}$次,
• B和小章出去了$\displaystyle \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}$次, 和小乙出去了$\displaystyle \frac{1}{2} \cdot \frac{1}{4} = \frac{1}{8}$次
• C和小乙出去了1次

归纳总结:

• A和小甲出去了$\displaystyle \frac{1}{4}$次, 和小乙出去了$\displaystyle \frac{1}{4}$次
• B和小甲出去了$\displaystyle \frac{1}{8}$次, 和小乙出去了$\displaystyle \frac{1}{8}$次, 和小章出去了$\displaystyle \frac{1}{2}$次
• C和小乙出去了1次

第二次迭代EM算法中的M步骤

• A和小甲, 小乙有问题的概率为$\displaystyle \frac{1/4}{1/4 + 1/4} = \frac{1}{2}$
• B和小甲, 小乙有问题的概率为$\displaystyle \frac{1/8}{1/8 + 1/8 + 1/2} = \frac{1}{6}$
• B和小章有问题的概率为$\displaystyle \frac{1/2}{1/8 + 1/8 + 1/2} = \frac{2}{3}$
• C和小乙有问题的概率为1

你继续计算，反思，总之，最后，你得到了真相。

通过上面的计算我们可以得知，EM算法实际上是一个不停迭代计算的过程，根据我们事先估计的先验概率A，得出一个结果B，再根据结果B，再计算得到结果A，然后反复直到这个过程收敛。
可以想象饭店的后方大厨，炒了两盘一样的菜，现在，菜炒好后从锅中倒入盘，不可能一下子就分配均匀，所以先往两盘中倒入，然后发现B盘菜少了，就从A中匀出一些，A少了，从B匀…..

EM算法

EM算法原理

给定m个训练样本${x(1), x(2), \cdots, x(m)}$, 样本间独立, 找出样本的模型参数$\theta$, 极大化模型参数的对数似然函数, 如下:

$$\theta = arg \max \limits_\theta \displaystyle \sum_{i=1}^{m} log(p(x^{(i)}; \theta))$$

假定样本中存在隐含数据$z={z(1), z(2), \cdots, z(k)}$, 此时极大化模型分布的对数似然函数如下:

$$\begin{align}\theta &= arg \max \limits_\theta \displaystyle \sum_{i=1}^{m} log(p(x^{(i)}; \theta))\\ &= arg \max \limits_\theta \displaystyle \sum_{i=1}^{m} log( \sum_{z^{(i)}} p(z^{(i)}) p(x^{(i)}|z^{(i)}; \theta) )\\ &= arg \max \limits_\theta \displaystyle \sum_{i=1}^{m} log( \sum_{z^{(i)}} p(x^{(i)}, z^{(i)}; \theta) )\\ \end{align}$$

Q(z)是一个随机变量的分布, 每一个取值对应的概率密度之和等于1.
$E(Y) = E(g(x)) = \sum_i g(x_i)p_i$, $\displaystyle \sum_z Q(z; \theta) = 1$

令z的分布为$Q(z; \theta)$, 并且$Q(z; \theta) \ge 0$, 那么如上的极大似然估计的最大化的函数$l(\theta)$

$$\begin{align} l(\theta) &= \displaystyle \sum_{i=1}^{m} log( \sum_{z^{(i)}} p(x^{(i)}, z^{(i)}; \theta) )\\ &= \displaystyle \sum_{i=1}^{m} log( \sum_{z^{(i)}} Q(z^{(i)}; \theta) \cdot \displaystyle \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q(z^{(i)}; \theta)} ) \\ &= \displaystyle \sum_{i=1}^{m} log( \quad \displaystyle E_Q( \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q(z^{(i)}; \theta)} ) \quad) \\ &\ge \displaystyle \sum_{i=1}^{m} E_Q ( \quad log( \displaystyle \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q(z^{(i)}; \theta)} ) \quad) \\ &\ge \displaystyle \sum_{i=1}^{m} \sum_{z^{(i)}} Q(z^{(i)}; \theta) (log( \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q(z^{(i)}; \theta)} ) ) \\ \end{align}$$

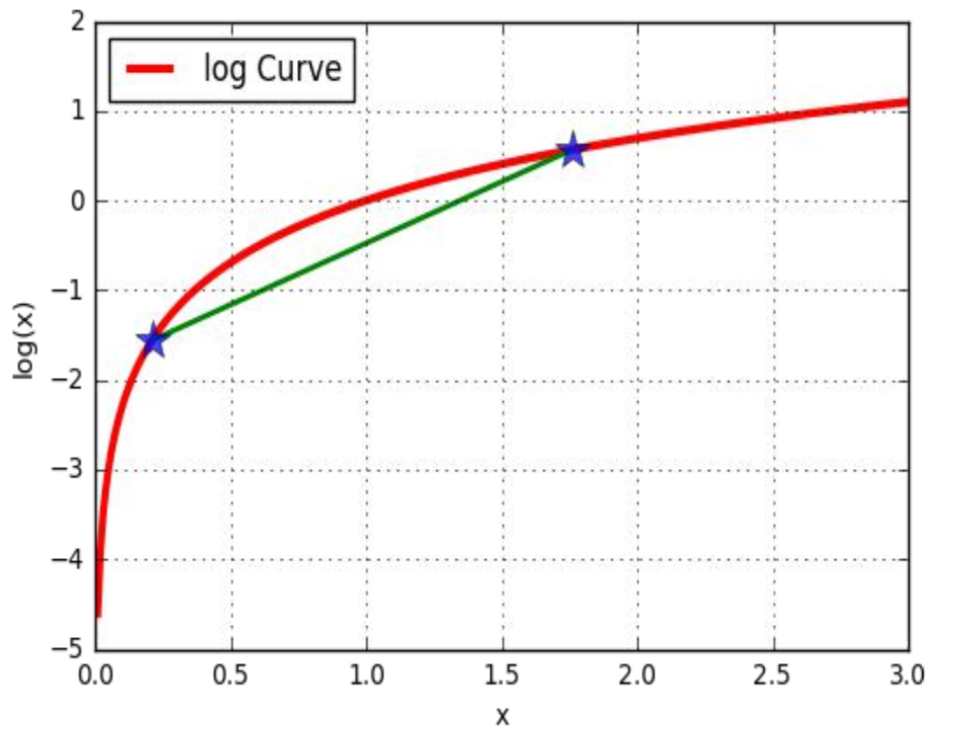
一般情况下, z是隐含变量, 不知道应该取多少合适, 但是可以通过最后得到的公式对z进行求解. 如果最后两步相等的话, 就用公式的最后一步去替代$l(\theta)$, 进而得到新公式的最大值. 那么最后两步在什么情况下才能相等?

根据不等式的性质, 当下面式子中的对数中的随机变量为常数的时候, $l(\theta)$和右边的式子取等号

$$\displaystyle \frac{p(x, z; \theta)}{Q(z; \theta)} = c, \quad \sum_zQ(z; \theta) = 1$$ $$\begin{align} Q(z; \theta) &= \frac{p(x, z; \theta)}{c} = \frac{p(x, z; \theta)}{c \cdot \displaystyle \sum_{z^{(i)}} Q(z^{(i)}; \theta)}\\ &=\frac{p(x, z; \theta)}{\displaystyle \sum_{z^{(i)}} c \cdot Q(z^{(i)}; \theta)} \\ &=\frac{p(x, z; \theta)}{\displaystyle \sum_{z^{(i)}} p(x, z^{(i)}; \theta)} \\ &=\frac{p(x, z; \theta)}{ p(x; \theta)} = p(z|x; \theta) \\ \end{align}$$

所以最后, 当$Q(z; \theta) = p(z|x; \theta)$的时候$l(\theta)$函数取得等号

$$\begin{align} \theta &= arg \max \limits_{\theta} l(\theta) = arg \max \limits_{\theta} \sum_{i=1}^{m} \sum_{z} Q(z; \theta^{old}) log( \frac{p(x, z; \theta)}{Q(z; \theta^{old})} )\\ &= arg \max \limits_{\theta} \sum_{i=1}^{m} \sum_{z} p(z|x; \theta^{old}) log( \frac{p(x, z; \theta)}{ p(z|x; \theta^{old}) } ) \\ &= arg \max \limits_{\theta} \sum_{i=1}^{m} \sum_{z} p(z|x; \theta^{old}) log( p(x, z; \theta) ) \\ \end{align}$$

EM算法流程

样本数据$X={x_1, x_2, \cdots, x_m}$, 联合分布$p(x, z; \theta)$, 条件分布$p(z|x; \theta)$, 最大迭代次数J

• 随机初始化模型参数$\theta$的初始值$\theta_0$
• 开始EM算法的迭代处理:
  • E步: 计算联合分布的条件概率期望, $Q^j = p(z|x; \theta^j) \quad l(\theta) = \displaystyle \sum_{i=1}^{m} \sum_z Q^j log(p(x, z; \theta^j))$
  • M步: 极大化L函数, 得到$\theta^{j+1}$, $\theta^{j+1} = arg \max \limits_{\theta} l(\theta)$
  • 如果$\theta^{j+1}$已经收敛, 则算法结束, 输出最终的模型参数$\theta$, 否则继续迭代处理

EM算法直观案例

假设现有两个装有不定数量黑球和白球的盒子, 随机从盒子中抽取出一个白球的概率分布为$p_1$和$p_2$; 为了估计这两个概率, 每次选择一个盒子, 有放回的连续随机抽取5个球, 记录如下:

盒子编号	1	2	3	4	5	统计
1	白	白	黑	白	黑	3白2黑
2	黑	黑	白	白	黑	2白3黑
1	白	黑	黑	黑	黑	1白4黑
2	白	黑	白	黑	白	3白2黑
1	黑	白	黑	白	黑	2白3黑

使用MLE最大似然估计:

$$l(p_1) = log(p_1^6(1-p_1)^9) = 6logp_1 + 9log(1-p_1)$$ $$\displaystyle \frac{\partial l(p_1)}{\partial p_1} = \frac{6}{p_1} - \frac{9}{1-p_1} \quad \underrightarrow{ 令\frac{\partial l(p_1)}{\partial p_1} = 0 } \quad p_1 = 0.4$$

同理

$$l(p_2) = log(p_2^5(1-p_2)^5) = 5logp_2 + 5log(1-p_2)$$ $$\displaystyle \frac{\partial l(p_2)}{\partial p_2} = \frac{5}{p_2} - \frac{5}{1-p_2} \quad \underrightarrow{ 令\frac{\partial l(p_2)}{\partial p_2} = 0 } \quad p_2 = 0.5$$

如果现在不知道具体的盒子编号, 但是同样还是为了求解$p_1$和$p_2$的值, 这个时候就相当于多了一个隐藏变量z, z表示每次抽取的时候选择的盒子编号, 比如$z_1$表示第一次抽取的时候选择的是盒子1还是盒子2

盒子编号	1	2	3	4	5	统计
z1	白	白	黑	白	黑	3白2黑
z2	黑	黑	白	白	黑	2白3黑
z3	白	黑	黑	黑	黑	1白4黑
z4	白	黑	白	黑	白	3白2黑
z5	黑	白	黑	白	黑	2白3黑

随机初始化一个概率值: $p_1=0.1$和$p_2=0.9$; 然后使用最大似然估计计算每轮操作中从两个盒子中抽取的最大概率. 然后使用计算出来的z值, 重新使用极大似然估计法估计概率值

$$L(z_1=1|x; p_1) = 0.1^3 * 0.9^2 = 0.00081$$ $$L(z_1=2|x; p_2) = 0.9^3 * 0.1^2 = 0.00729$$

轮数	盒子1	盒子2
1	0.00081	0.00729
2	0.00729	0.00081
3	0.06561	0.00009
4	0.00081	0.00729
5	0.00729	0.00081

在这里, 切记$p_1$表示从盒子1中抽取到白球的概率, $p_2$表示从盒子2中抽取到白球的概率, 那么上述表格就表示第1轮从盒子2中抽取的概率较大, 第2轮从盒子1中抽取的概率较大, 总结一下就是第1, 4轮从盒子1中抽取的概率较大, 第2, 3, 5轮从盒子2中抽取的概率较大

那么更新一下原始表格如下:

盒子编号	1	2	3	4	5	统计
2	白	白	黑	白	黑	3白2黑
1	黑	黑	白	白	黑	2白3黑
1	白	黑	黑	黑	黑	1白4黑
2	白	黑	白	黑	白	3白2黑
1	黑	白	黑	白	黑	2白3黑

根据此表格, 得出$p_2=\frac{6}{10}=0.6, \quad p_1=\frac{5}{15}=\frac{1}{3}$

$$L(z_1=1|x; p_1) = (\frac{1}{3})^3 * 0.6^2 = 0.01565$$ $$L(z_1=2|x; p_2) = 0.6^3 * (\frac{1}{3})^2 = 0.03456$$

轮数	盒子1	盒子2
1	0.01565	0.03456
2	0.0313	0.02304
3	0.0626	0.01536
4	0.01565	0.03456
5	0.0313	0.02304

使用最大似然概率法则估计z和p的值, 但是在这个过程中, 只使用一个最有可能的值. 如果考虑所有的z值, 然后对每一组z值都估计一个概率p, 那么这个时候估计出来的概 率可能会更好, 可以用期望的方式来简化这个操作

归一化操作

轮数	盒子1	盒子2
1	0.00081/(0.00081+0.00729) = 0.1	0.00729/(0.00081+0.00729) = 0.9
2	0.00729	0.00081
3	0.06561	0.00009
4	0.00081	0.00729
5	0.00729	0.00081

EM算法收敛证明

EM算法的收敛性只要能够证明对数似然函数的值在迭代过程中是增加的就可以

$$\displaystyle \sum_{i=1}^{m}log(p(x^i; \theta^{j+1})) \ge \sum_{i=1}^{m}log(p(x^i; \theta^{j}))$$

构造函数如下:

$$L(\theta, \theta^j) = \sum_{i=1}^{m} \sum_z p(z|x^i; \theta^j) log(p(x^i, z; \theta))$$ $$H(\theta, \theta^j) = \sum_{i=1}^{m} \sum_z p(z|x^i; \theta^j) log(p(z|x^i; \theta))$$ $$\because \sum_z p(z|x^i; \theta^j) = 1$$ $$\begin{align} \therefore L(\theta, \theta^j) - H(\theta, \theta^j) &= \sum_{i=1}^{m} \sum_z p(z|x^i; \theta^j) log(\frac{p(x^i, z; \theta)}{p(z|x^i; \theta}) \\ &= \sum_{i=1}^{m} log(\frac{p(x^i, z; \theta)}{p(z|x^i; \theta})\\ &= \sum_{i=1}^{m} log(p(x^i; \theta))\\ \end{align}$$ $$\begin{align} \therefore [L(\theta^{j+1}, \theta^j) - H(\theta^{j+1}, \theta^j)] - [L(\theta^{j}, \theta^j) - H(\theta^{j}, \theta^j)] &= [L(\theta^{j+1}, \theta^j) - L(\theta^{j}, \theta^j)] - [H(\theta^{j+1}, \theta^j) - H(\theta^{j}, \theta^j)] \\ &= \sum_{i=1}^{m} log(p(x^i; \theta^{j+1})) - \sum_{i=1}^{m} log(p(x^i; \theta^j))\\ \end{align}$$

而

$$\begin{align} L(\theta^{j+1}, \theta^j) - L(\theta^{j}, \theta^j) &= \sum_{i=1}^{m} \sum_z p(z|x^i; \theta^j) log(p(x^i, z; \theta^{j+1})) - \sum_{i=1}^{m} \sum_z p(z|x^i; \theta^j) log(p(x^i, z; \theta^j)) \\ &= \sum_{i=1}^{m} \sum_z p(z|x^i; \theta^j) log( \frac{p(x^i, z; \theta^{j+1})}{p(x^i, z; \theta^j)} )\\ & \ge 0 \\ \end{align}$$ $$\begin{align} H(\theta^{j+1}, \theta^j) - H(\theta^{j}, \theta^j) &= \sum_{i=1}^{m} \sum_z p(z|x^i; \theta^j) log(p(z|x^i; \theta^{j+1})) - \sum_{i=1}^{m} \sum_z p(z|x^i; \theta^j) log(p(z|x^i; \theta^j)) \\ &= \sum_{i=1}^{m} \sum_z p(z|x^i; \theta^j) log( \frac{p(z|x^i; \theta^{j+1})}{p(z|x^i; \theta^j)}) \\ &\because log函数是开口向下的凸函数 \\ &\therefore \le \sum_{i=1}^{m} log( \sum_z p(z|x^i; \theta^j) \frac{p(z|x^i; \theta^{j+1})}{p(z|x^i; \theta^j)}) = 0 \\ \end{align}$$ $$\sum_{i=1}^{m} log(p(x^i; \theta^{j+1})) - \sum_{i=1}^{m} log(p(x^i; \theta^j)) \ge 0$$

然而如下问题
随机选择1000名用户, 测量用户的身高; 若样本中存在男性和女性, 身高分别服从高斯分布$N(\mu_1, \sigma_1)$和$N(\mu_2, \sigma_2)$的分布, 试估计参数: $\mu_1, \sigma_1, \mu_2, \sigma_2$;

解析:

• 如果明确的知道样本的情况(即男性和女性数据是分开的), 那么我们使用极大似然估计来估计这个参数值
• 如果样本是混合而成的, 不能明确的区分开, 那么就没法直接使用极大似然估计来进行参数的估计. 可以使用EM算法来估计男女这两个参数值, 即男女这两个性别就变成了隐含变量. 实际上, EM算法在某些层面上是在帮助我们做聚类的操作. 即帮助我们找到隐含变量的取值.

GMM

GMM(Gaussian Mixture Model), 高斯混合模型, 是指该算法由多个高斯模型线性叠加混合而成, 每个高斯模型称为component. GMM算法描述的是数据本身存在的一种分布
GMM常用于聚类应用中, component的个数就可以认为是类别的数量
假定GMM由k个Gaussian分布线性叠加而成, 那么概率密度函数如下:

$$p(x) = \sum_{k=1}^{K}p(k)p(x|k) = \sum_{k=1}^{K} \pi_k p(x; \mu_k, \sum_k)$$

对数似然函数

$$l(\pi, \mu, \sigma) = \displaystyle \sum_{i=1}^{N} log( \sum_{k=1}^{K}\pi_k p(x^i; \mu_k, \sum_k) )$$

E step

$$w_{j}^{(i)} = Q_i(z^{(i)} = j) = p(z^{(i)} = j|x^{(i)}; \pi, \mu, \sum)$$

M step

$$\begin{align} l(\pi, \mu, \sum) &= \sum_{i=1}^{m} \sum_{z^{(i)}} Q_i(z^{(i)}) log( \frac{p(x^{(i)}, z^{(i)}; \pi, \mu, \sum)}{Q_i(z^{(i)})} ) \\ &= \sum_{i=1}^{m} \sum_{j=1}^{k} Q_i(z^{(i)=j}) log( \frac{p(x^{(i)}|z^{(i)}=j; \mu, \sum) \cdot p(z^{(i)}=j; \pi)}{Q_i(z^{(i)}=j)} ) \\ &= \sum_{i=1}^{m} \sum_{j=1}^{k} w_j^{(i)} log( \frac{ \frac{1}{ (2\pi)^{\frac{n}{2}} \vert \sum_j \vert^{ \frac{1}{2} } } e^{-\frac{1}{2} (x^{(i)}-\mu_j)^T \sum_j^{-1}(x^{(i)}-\mu_j) \cdot \pi_j} }{w_j^{(i)}} ) \\ \end{align}$$

对均值求偏导

$$l(\pi, \mu, \sum) = \sum_{i=1}^{m} \sum_{j=1}^{k} w_j^{(i)}(-\frac{1}{2}(x^{(i)}-\mu_j)^T \sum_j^{-1}(x^{(i)}-\mu_j)) + c$$

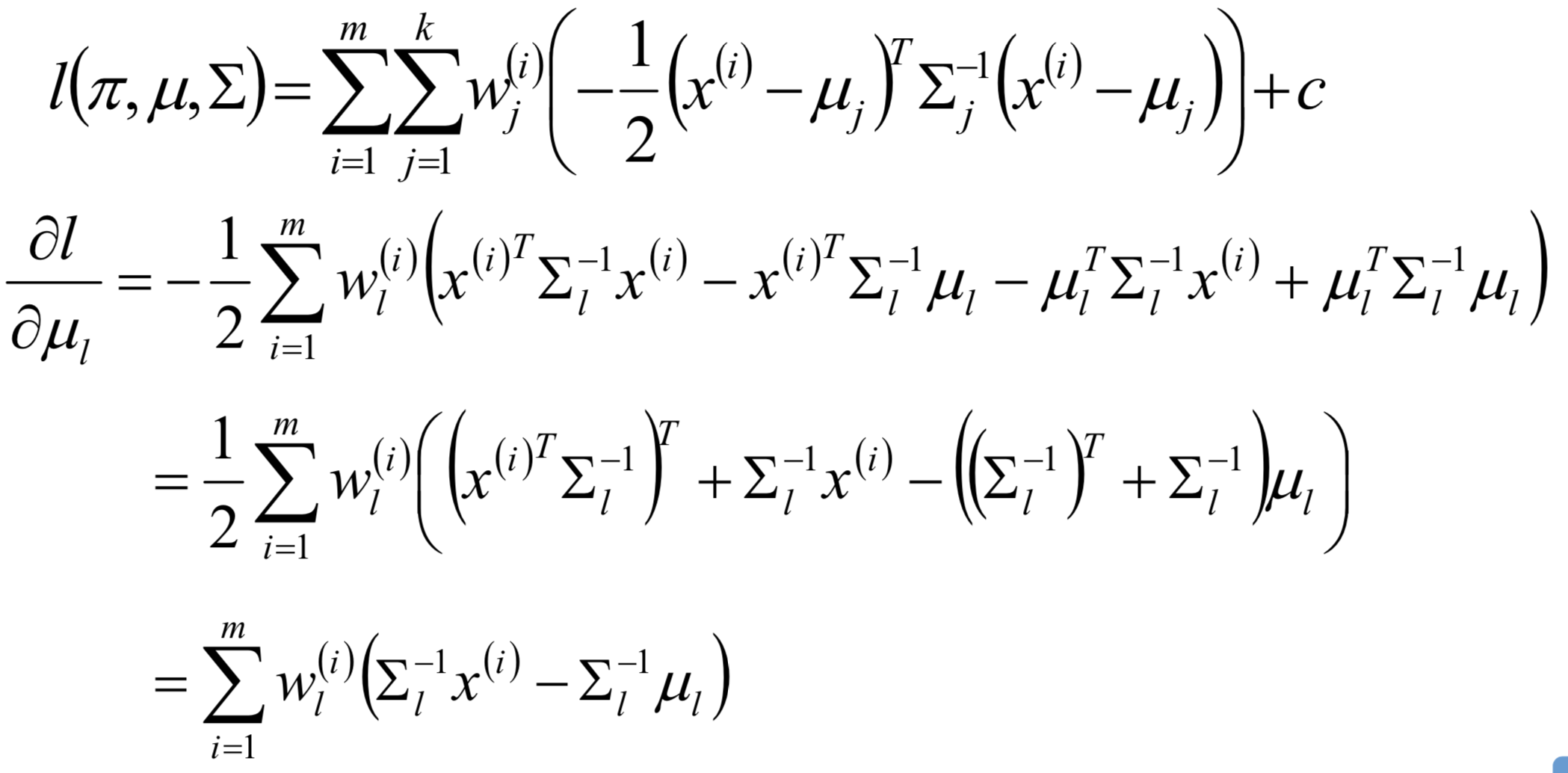
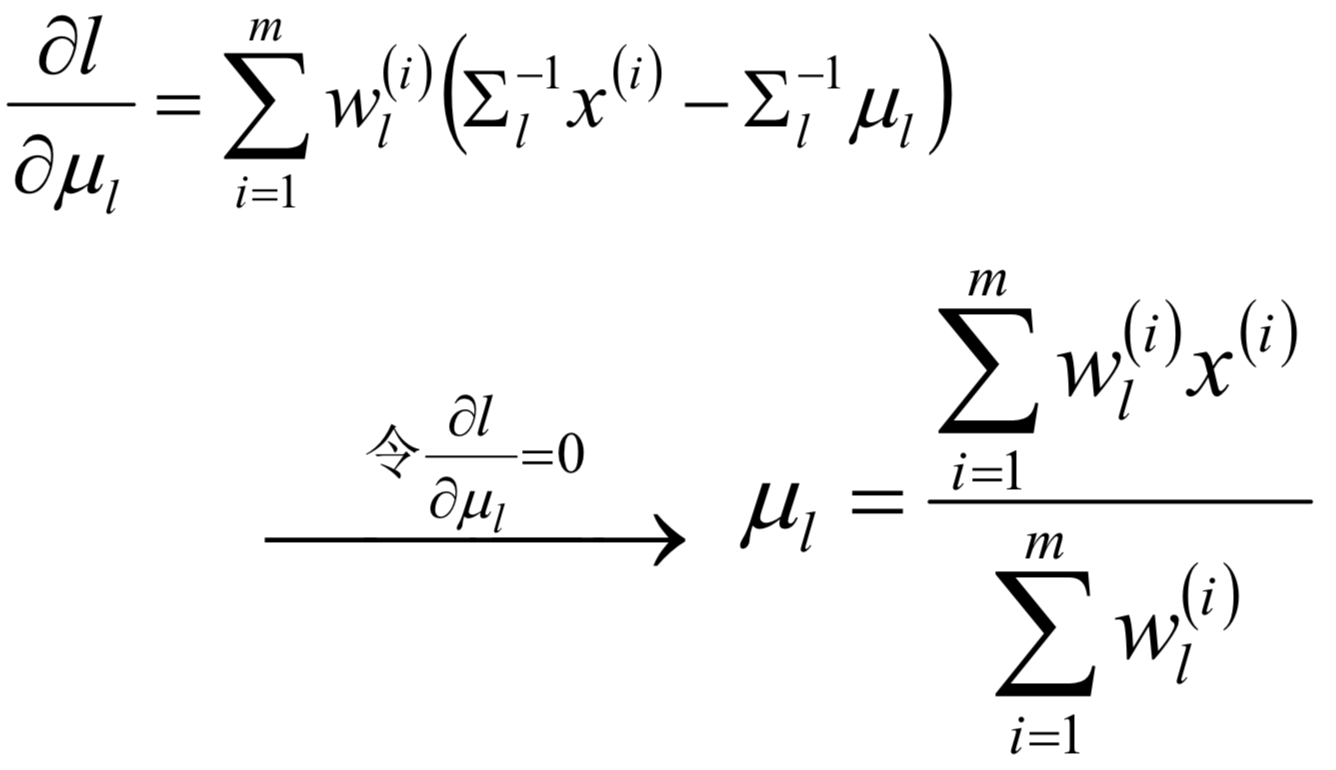
对方差求偏导

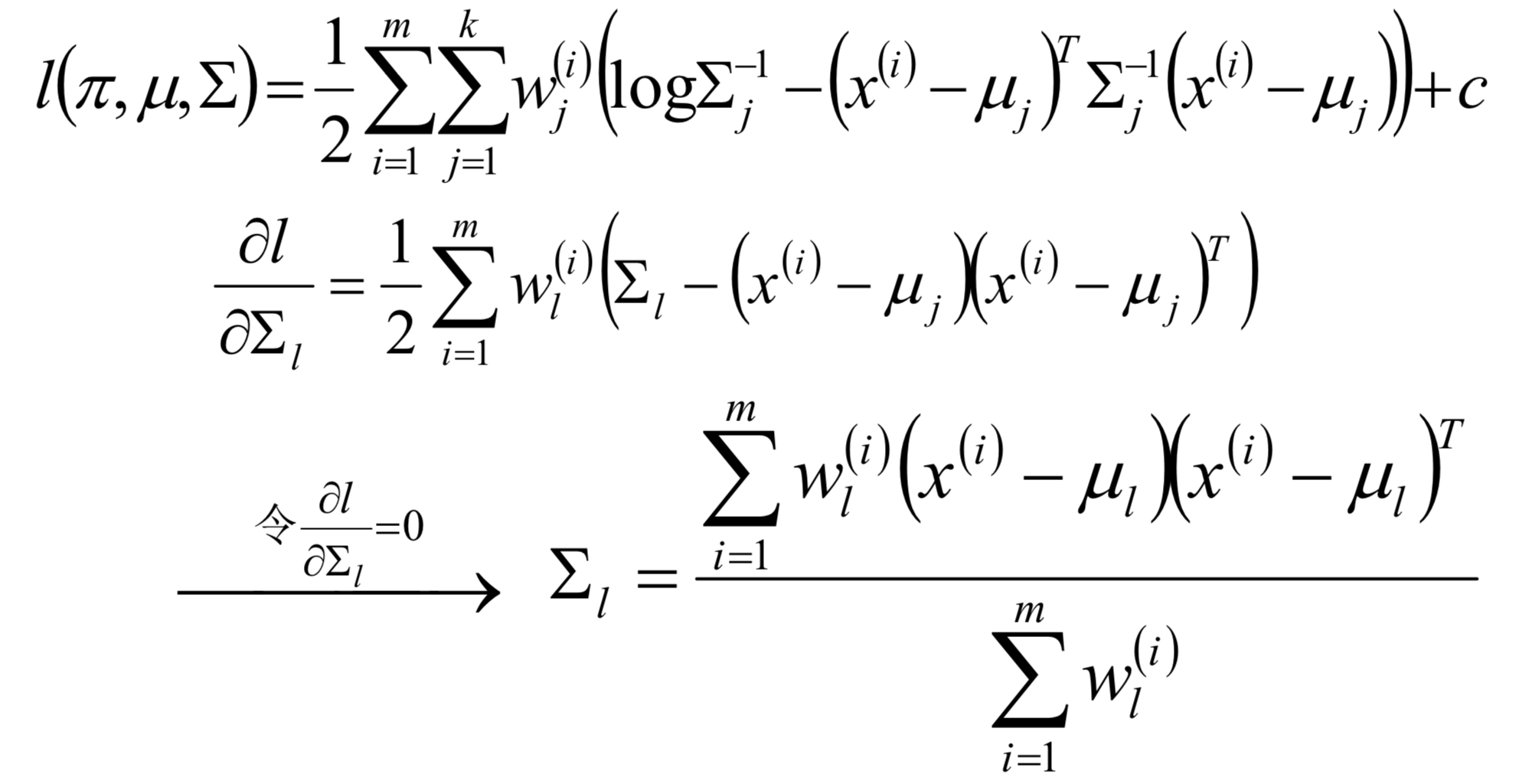
对概率使用拉格朗日乘子法求解

多分类及多标签分类

单标签二分类

单标签多分类

多标签分类算法