L9

马尔可夫性质

设$\{X(t), t \in T\}$是一个随机过程, E是其状态空间, 若对于任意的$t_1 < t_2 < \cdots < t_n < t$, 任意的$x_1 < t_2 < \cdots < t_n < t$, 任意的$x_1, x_2, \cdots, x_n, x \in E$, 随机变量$X(t)$在已知变量$X(t_1) = x_1, \cdots, X(t_n) = x_n$下的条件分布函数只与$X(t_n)=x_n$有关, 而与$X(t_1)=x_1, \cdots, X(t_{n-1})=x_{n-1}$无关, 即条件分布函数满足下列等式, 此性质称为马尔可夫性质; 如果随机过程满足马尔可夫性质, 则该过程称为马尔可夫过程.

$$p(X(t) \le x | X(t_1)=x_1, \cdots, X(t_n)=x_n) = p(X(t) \le x | X(t_n) = x_n)$$ $$p(X_{n+1}=x| X_1=x_1, \cdots, X_n=x_n) = p(X_{n+1} | X_n = x_n)$$

马尔可夫链

马尔可夫链是指具有马尔可夫性质的随机过程. 在过程中, 在给定当前信息的情况下, 过去的信息状态对于预测未来状态是无关的.

在马尔可夫链的每一步, 系统根据概率分布, 可以从一个状态变成另外一个状态, 也可以保持当前状态不变. 状态的改变叫做转移, 状态改变的相关概率叫做转移概率

马尔可夫链中的三元素是: 状态空间S, 转移概率矩阵P, 初始概率分布$\pi$

HMM

隐马尔可夫模型(Hidden Markov Model, HMM)是一种统计模型, 在语音识别, 行为识别, NLP, 故障诊断等领域具有高效的性能.

HMM是关于时序的概率模型, 描述一个含有未知参数的马尔可夫链所生成的不可观测的状态随机序列, 再由各个状态生成观测随机序列的过程. HMM是一个双重随机过程, 具有一定状态的隐马尔可夫链和随机的观测序列.

HMM随机生成的状态随机序列被称为状态序列; 每个状态生成一个观测, 由此产生的观测随机序列被称为观测序列.

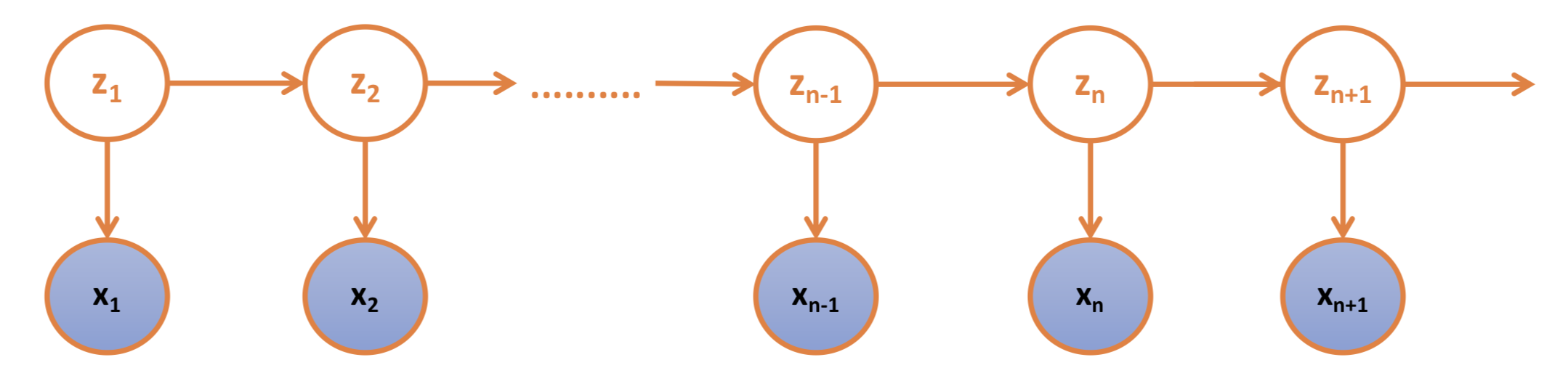
$z_1, z_2, \cdots, z_n$是不可观测的状态, $x_1, x_2, \cdots, x_n$是可观测到的序列; 不可观测的状态决定可观测序列的值(z的取值决定x的取值)

HMM由隐含状态S, 可观测状态O, 初始状态概率矩阵$\pi$, 隐含状态转移概率矩阵A, 可观测值转移概率矩阵B(也称为混淆矩阵, Confusion Matrix)

$\pi$和A决定了状态序列, B决定观测序列, 因此HMM可以使用三元符号表示, 称为HMM三元素

$$\lambda = (A, B, \pi)$$

HMM参数说明

HMM模型 $\lambda = (A, B, \pi)$

S是所有可能的状态集合

$$S = \{ S_1, S_2, \cdots, S_n\}$$

O是所有可能的观测集合

$$O = \{ O_1, O_2, \cdots, O_n \}$$

I是长度为T的状态序列, Q对应的观测序列

$$I = \{ i_1, i_2, \cdots, i_T \} \qquad Q = \{ q_1, q_2, \cdots, q_T \}$$

A是隐含状态转移概率矩阵

$$A = [a_{ij}]_{n \ast n} = \begin{bmatrix} {a_{11}}&{a_{12}}&{\cdots}&{a_{1n}}\\ {a_{21}}&{a_{22}}&{\cdots}&{a_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {a_{n1}}&{a_{n2}}&{\cdots}&{a_{nn}}\\ \end{bmatrix}$$

其中$a_{ij} = a_{i_t i_{t+1}}= p(i_{t+1}=s_j | i_t = s_i)$, 表示在时刻$t$处于状态序列中$s_i$状态的条件下时刻$t+1$转移到状态$s_j$的概率

B是可观测值转移概率矩阵

$$B = [b_{ij}]_{n \ast m} = \begin{bmatrix} {b_{11}}&{b_{12}}&{\cdots}&{b_{1m}}\\ {b_{21}}&{b_{22}}&{\cdots}&{b_{2m}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {b_{n1}}&{b_{n2}}&{\cdots}&{b_{nm}}\\ \end{bmatrix}$$

其中$b_{ij} = b_{i_t q_t} = p( q_t = o_j | i_t=s_i)$, 表示在时刻$t$处于状态序列中$s_i$状态的条件下, 生成可观测状态$o_j$的概率

$\pi$是初始状态概率向量

$$\pi = (\pi_i)_{1 \ast n} = (\pi_1, \pi_2, \cdots, \pi_n)$$

其中$\pi_{i_1} = p(i_1 = s_i)$, 表示在时刻$t=1$处于状态序列中$s_i$的概率

HMM的两个性质

$$p(i_{t} | i_{t-1}, q_{t-1}, i_{t-2}, q_{t-2}, \cdots, i_1, q_1) = p(i_{t} | i_{t-1})$$ $$p(q_{t} | i_t, i_{t-1}, q_{t-1}, i_{t-2}, q_{t-2}, \cdots, i_1, q_1) = p(q_{t} | i_t)$$

看这个意思就是当前状态的概率只和上一个状态的概率有关, 与其他都没有关系

HMM案例

假设有三个盒子, 编号分别为1, 2, 3; 每个盒子都装有黑白两种颜色的小球, 小球的比例如下:

编号	白球	黑球
1	4	6
2	8	2
3	5	5

• 按照$\pi$的概率选择一个盒子, 从盒子中随机抽取一个小球, 记录颜色后, 放回盒子中
• 按照某种条件概率选择新的盒子, 重复该操作
• 最终得到的观测序列为: “白黑白白黑”

对该题目的理解如下:

有放回的按照概率$\pi$来抽取, 假如第一次抽取的是1号盒子, 第二次抽取的是3号盒子, 接下来是2号, 2号, 3号, 举个例子, 所以

3号 -> 2号 -> 1号 -> 1号 -> 2号, 状态序列
白球 -> 黑球 -> 白球 -> 白球 -> 黑球, 观测序列

HMM的的三个问题

• 概率计算问题
  给定模型$\lambda=(A, B, \pi)$和观测序列$Q = \{q_1, q_2, \cdots, q_T\}$, 利用前向-后向算法计算模型$\lambda$之下观测到序列Q出现的概率
• 学习问题
  已知观测序列$Q = \{q_1, q_2, \cdots, q_T\}$, 使用Baum-Welch算法估计模型$\lambda=(A, B, \pi)$的参数, 使得在该模型下观测序列$p(Q|\lambda)$最大
• 预测问题
  给定模型$\lambda=(A, B, \pi)$和观测序列$Q = \{q_1, q_2, \cdots, q_T\}$, 利用Viterbi算法求解给定观测序列条件概率$p(I|Q, \lambda)$的最大状态序列$I$

概率计算问题

直接计算法/暴力算法

给定模型$\lambda=(A, B, \pi)$和观测序列$Q = \{q_1, q_2, \cdots, q_T\}$, 计算在模型$\lambda$的情况下, 得到观测序列Q出现的概率$p(Q; \lambda)$

要想得到观测序列”白球 -> 黑球 -> 白球 -> 白球 -> 黑球”这样的结果, 又因为每个盒子都是有白球和黑球的, 然而我们并不知道状态序列及抽取的盒子的序列是什么样的, 所以如下:

按照概率公式, 列举所有可能的长度为T的状态序列$I = \{ i_1, i_2, \cdots, i_T\}$, 先求出各个状态序列与观测序列$Q=\{q_1, q_2, \cdots, q_T\}$的联合概率$P(Q,I; \lambda)$, 然后对所有可能的状态序列求和, 从而得到最后的概率$p(Q;\lambda)$

$$I = \{ i_1, i_2, \cdots, i_T\} \qquad p(I;\lambda) = \pi_{i_1} a_{i_1 i_2} a_{i_2 i_3} \cdots a_{i_{T-1} i_T}$$ $$Q = \{ q_1, q_2, \cdots, q_T\} \qquad p(Q | I;\lambda) = b_{i_1 q_1} b_{i_2 q_2} \cdots b_{i_T q_T}$$ $$p(Q, I; \lambda) = p(Q | I;\lambda) p(I;\lambda) = \pi_{i_1} a_{i_1 i_2 } a_{i_2 i_3} \cdots a_{i_{T-1} i_T} \ast b_{i_1 q_1} b_{i_2 q_2} \cdots b_{i_T q_T}$$ $$p(Q; \lambda) = \sum_I p(Q, I; \lambda) = \sum_I \pi_{i_1} a_{i_1 i_2 } a_{i_2 i_3} \cdots a_{i_{T-1} i_T} \ast b_{i_1 q_1} b_{i_2 q_2} \cdots b_{i_T q_T}$$

假设抽取盒子的状态序列 $I = 3号, 2号, 1号, 1号, 2号$, 那么该状态序列的长度$T = 5$

$$\therefore p(I; \lambda) = \pi_3 a_{32} a_{21} a_{11} a_{12}$$ $$\therefore p(Q | I; \lambda) = b_{3白} b_{2黑} b_{1白} b_{1白} b_{2黑}$$ $$\therefore p(Q, I; \lambda) = p(Q | I;\lambda) p(I;\lambda) = \lambda) = \pi_3 a_{32} a_{21} a_{11} a_{12} \ast b_{3白} b_{2黑} b_{1白} b_{1白} b_{2黑}$$

上述只是求出了一种盒子的状态序列, 因为每个盒子里边既有白球又有黑球, 所以盒子的状态序列总共有$3^5$种可能.

然后对所有可能的状态序列求和

前向概率/后向概率

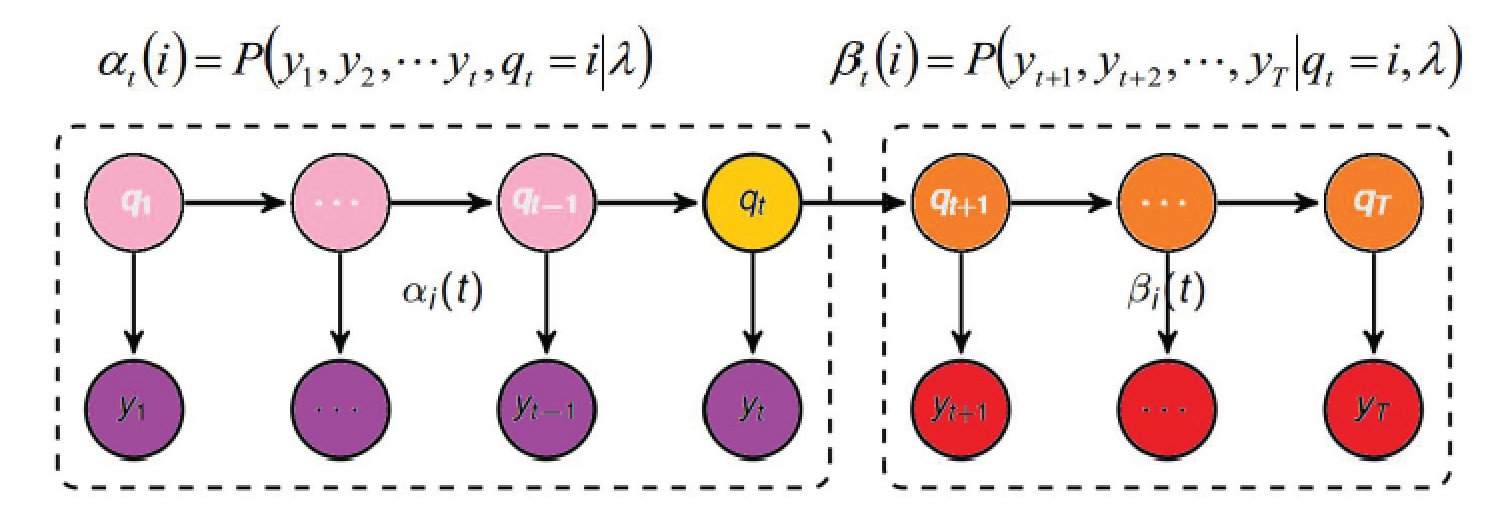
$\alpha_t$是给定$q_t$, 时刻1到时刻t所有观测值$y_1, y_2, \cdots, y_t, q_t$出现的联合概率
$\beta_t$是给定$q_t$, 时刻t+1到时刻T, 所有观测值$y_{t+1}, y_{t+2}, \cdots, y_T$出现的联合概率

$$\alpha_t(i) = p(y_1, y_2, \cdots, y_t, q_t = i | \lambda)$$ $$\beta_t(i) = p(y_{t+1}, y_{t+2}, \cdots, y_T | q_t = i, \lambda)$$

前向概率-后向概率指的是在一个观测序列中, 时刻t对应状态$s_i$的概率值转换过来的信息

$$\begin{align} p(q_1, q_2, \cdots, q_T, i_t=s_i) &= p(q_1, q_2, \cdots, q_{t}, q_{t+1}, q_{t+2}, \cdots, q_T, i_t=s_i) \\ &= p(q_1, q_2, \cdots, q_t, i_t=s_i) \ast p(q_{t+1}, q_{t+2}, \cdots, q_T | q_1, q_2, \cdots, q_t, i_t=s_i)\\ &= p(q_1, q_2, \cdots, q_t, i_t=s_i) \ast p(q_{t+1}, q_{t+2}, \cdots, q_T | i_t=s_i ) \\ &= p(q_1, q_2, \cdots, q_t, i_t=s_i; \lambda) \ast p(q_{t+1}, q_{t+2}, \cdots, q_T | i_t=s_i; \lambda) \\ \end{align}$$

前向算法

给定$\lambda$, 定义前向概率为, 在时刻t观测序列为$q_1, q_2, \cdots, q_t$, 状态序列的当前状态为$s_i$的概率, 记为:

$$\alpha_t(i) = p(q_1, q_2, \cdots, q_t, i_t=s_i; \lambda)$$

初值$\alpha_1(i) = p(q_1, i_1=s_i; \lambda) = \pi_i b_{i q_1}$, 表示在时刻$t=1$, 观测序列为$q_1$和状态序列的当前状态为$s_i$的联合概率

$$\begin{align} \alpha_1(i) &= p(q_1, i_1=s_i; \lambda)\\ &= p(i_1=s_1 | q_1; \lambda) \ast p(q_1; \lambda) \\ &= p(i_1=s_1; \lambda) \ast p(q_1 = o_j| i_1 = s_i; \lambda) \\ &= \pi_{i_1} b_{i_1 q_1} \end{align}$$

递推: 对于$t=1, 2, \cdots, T-1$

$$\alpha_{t+1}(i) = (\displaystyle \sum_{j=1}^n \alpha_t(j) a_{ji}) b_{i q_{t+1}}$$

最终

$$p(Q; \lambda) = \displaystyle \sum_{i=1}^n \alpha_T(i)$$ $$\begin{align} \alpha_t(i) &= p(q_1, q_2, \cdots, q_{t-1}, q_t, i_t=s_i) \\ &= p(q_1, q_2, \cdots, q_{t-1}, i_t = s_i) \ast p(q_t | q_1, q_2, \cdots, q_{t-1}, i_t = s_i) \\ &= p(q_1, q_2, \cdots, q_{t-1}, i_t = s_i) \ast p(q_t | i_t = s_i) \\ &= [\displaystyle \sum_{j=1}^n p(q_1, q_2, \cdots, q_{t-1}, i_{t-1} = s_j, i_t = s_i)] \ast p(q_t | i_t = s_i) \\ &= [\displaystyle \sum_{j=1}^n p(q_1, q_2, \cdots, q_{t-1}, i_{t-1} = s_j) \ast p( i_t = s_i | i_{t-1} = s_j)] \ast p(q_t | i_t = s_i) \\ &= (\displaystyle \sum_{j=1}^n \alpha_{t-1}(j) a_{ji}) \ast b_{i_t q_t} \\ \end{align}$$

后向算法

给定$\lambda$, 定义后向概率为, 在时刻t状态序列的当前状态为$s_i$的前提下, 从时刻$t+1$到时刻T部分的观测序列为$q_{t+1}, q_{t+2}, \cdots, q_T$的概率, 记为:

$$\beta_t(i) = p(q_{t+1}, q_{t+2}, \cdots, q_T | i_t=s_i; \lambda)$$

初值: $\beta_T(i) = 1$, 根据$\beta_t(i)$的公式, 令$t=T$, 那么整个状态序列和观测序列总共只有T个时刻, 是不可能有$T+1$时刻的, 所以$T+1$时刻之后发生的是必然事件, 所以$\beta_T(i) = 1$
递推: 对于$t = T-1, T-2, \cdots, 1$, 倒着推导

$$\beta_t(i) = \displaystyle \sum_{j=1}^n (a_{ij} b_{j q_{t+1}} \beta_{t+1}(j))$$

最终

$$p(Q; \lambda) = \displaystyle \sum_{i=1}^n \pi_i b_{i q_1} \beta_1(i)$$

根据上述$\beta_t$的定义, $\beta_t(i)$是给定$q_t$, 时刻$t+1$到时刻$T$, 所有观测值$y_{t+1}, y_{t+2}, \cdots, y_T$的联合概率, 如下图所示: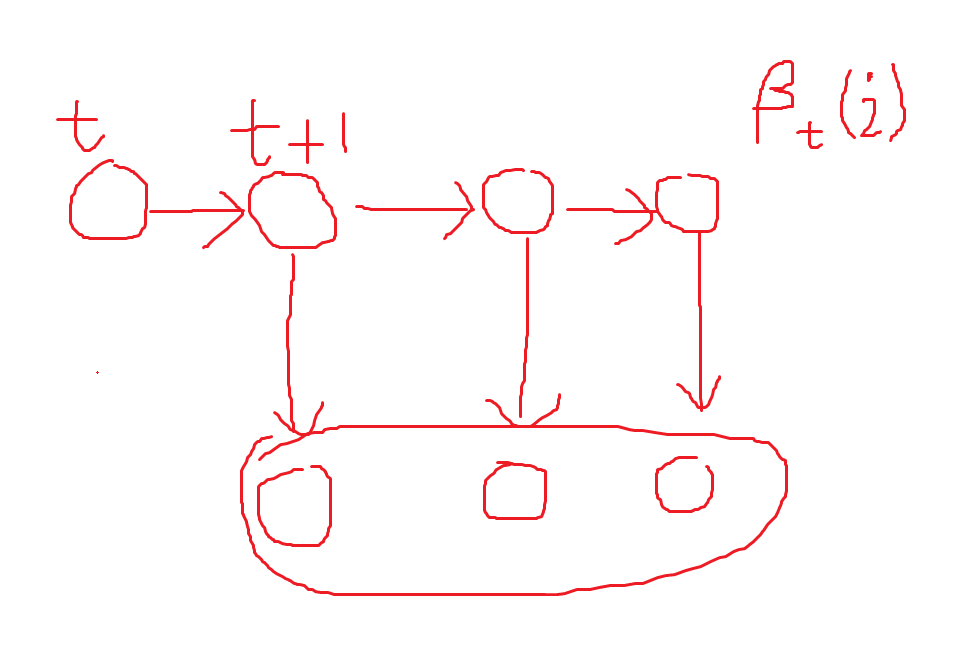

那么$\beta_{t+1}(i)$就是给定$q_t$(这里为什么不是$q_{t+1}$), 时刻$t+2$到时刻$T$, 所有观测值$y_{t+2}, \cdots, y_T$的联合概率, 如下图所示: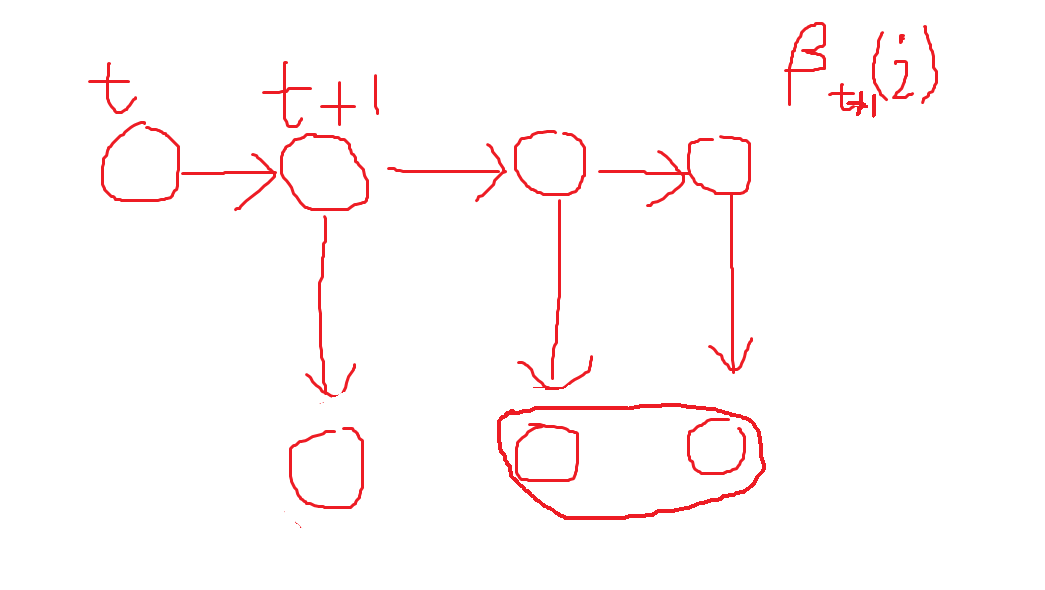

$$\begin{align} \beta_t(i) &= p(q_{t+1}, q_{t+2}, \cdots, q_T | i_t=s_i) \\ &= \displaystyle \sum_{j=1}^n p(i_{t+1} = s_j, q_{t+1}, q_{t+2}, \cdots, q_T | i_t = s_i) \\ &= \displaystyle \sum_{j=1}^n p(q_{t+1}, q_{t+2}, \cdots, q_T | i_{t+1} = s_j) \ast p(i_{t+1}=s_j | i_t=s_i) \\ &= \displaystyle \sum_{j=1}^n p(q_{t+2}, \cdots, q_T | i_{t+1} = s_j) \ast p(q_{t+1} | i_{t+1}=s_j) \ast p(i_{t+1}=s_j | i_t=s_i) \\ &= \displaystyle \sum_{j=1}^n (a_{ij} b_{j q_{t+1}} \beta_{t+1}(j)) \\ \end{align}$$

单个状态的概率

求给定模型$\lambda$和观测序列Q的情况下, 在时刻t处于状态序列中$s_i$的概率, 计作:

$$\gamma_t(i) = p(i_t=s_i|Q;\lambda)$$

单个状态概率的意义主要是用于判断在每个时刻最可能存在的状态序列中的状态, 从而可以得到整个状态序列作为最终的预测结果

$$p(i_t=s_i, Q;\lambda) = \alpha_t(i)\beta_t(i)$$ $$\begin{align} \gamma_t(i) = p(i_t=s_i|Q;\lambda) &= \frac{p(i_t=s_i, Q; \lambda)}{p(Q;\lambda)} \\ &= \frac{\alpha_t(i)\beta_t(i)}{p(Q;\lambda)}=\frac{\alpha_t(i)\beta_t(i)}{\displaystyle \sum_{j=1}^n\alpha_t(j)\beta_t(j)} \\ \end{align}$$

两个状态的联合概率

求给定模型$\lambda$和观测序列Q的情况下, 在时刻t处于状态$s_i$并且在时刻$t+1$处于状态$s_j$概率, 计作:

$$\begin{align} \xi_t(i, j) &= p(i_t=s_i, i_{t+1}=s_j|Q;\lambda) \\ &= \frac{p(i_t=s_i, i_{t+1}=s_j, Q; \lambda)}{p(Q; \lambda)} \\ &= \frac{ p(i_t=s_i, i_{t+1}=s_j, Q; \lambda) }{ \displaystyle \sum_{i=1}^n \sum_{j=1}^n p(i_t=s_i, i_{t+1}=s_j, Q;\lambda ) } \\ \end{align}$$ $$p(i_t=s_i, i_{t+1}=s_j, Q; \lambda) = \alpha_t(i) a_{ij} b_{j q_{t+1}} \beta_{t+1}(j)$$

学习问题

若训练数据包含观测序列和状态序列, 则HMM的学习问题非常简单, 是监督学习算法
若训练数据值包含观测序列, 则HMM的学习问题需要使用EM算法求解, 是非监督学习算法

学习问题-监督学习

直接利用大数定理的结论”频率的极限是概率”, 直接给出HMM的参数估计

$$\hat \pi_i = \frac{ \vert s_i \vert}{ \displaystyle \sum_{i=1}^n \vert s_i \vert }$$ $$a_{ij} = \frac{\vert s_{ij} \vert}{ \displaystyle \sum_{j=1}^n \vert s_{ij} \vert }$$ $$\hat b_{ij} = \frac{\vert q_{ij} \vert}{ \displaystyle \sum_{j=1}^n \vert q_{ij} \vert }$$

学习问题-非监督学习

预测问题

近似算法

直接在每个时刻t时候最有可能的状态作为最终的预测状态, 使用下列公式计算概率值

$$\gamma_t(i) = \frac{\alpha_t(i) \beta_t(i)}{p(Q; \lambda)} = \frac{ \alpha_t(i)\beta_t(i) }{ \displaystyle \sum_{j=1}^n \alpha_t(j)\beta_t(j) }$$

viterbi算法

viterbi算法实际是用动态规划的思路求解HMM预测问题, 求概率最大的”路径”, 每条”路径”对应一个状态序列

$$\delta_t(i) = \max \limits_{i_1, i_2, \cdots, i_{t-1}} p(i_t=i, i_1, i_2, \cdots, i_{t-1}, q_t, q_{t-1}, \cdots, q_1; \lambda)$$ $$\delta_1(i) = \pi_i b_{i q_1}$$ $$\delta_{t+1}(i) = \max \limits_{ 1 \le j \le n} (\delta_t(j)a_{ji}) b_{i q_{t+1}}$$ $$p^{\ast} = \max \limits_{ 1 \le j \le n} \delta_T(i)$$

viterbi算法案例

给定参数$\pi, A, B$, 得到观测序列为”白黑白白黑”, 求出最优的隐藏状态序列

$$\pi = \begin{bmatrix} {0.2}\\ {0.5}\\ {0.3}\\ \end{bmatrix}$$ $$A = \begin{bmatrix} {0.5}&{0.4}&{0.1}\\ {0.2}&{0.2}&{0.6}\\ {0.2}&{0.5}&{0.3}\\ \end{bmatrix}$$ $$B = \begin{bmatrix} {0.4}&{0.6}\\ {0.8}&{0.2}\\ {0.5}&{0.5}\\ \end{bmatrix}$$ $$\delta_1(i) = \pi_i b_{i q_1} = \pi_i b_{i白 }$$ $$\delta_1(1) = 0.2 * 0.4 = 0.08 \qquad \delta_1(2) = 0.5 * 0.8 = 0.4 \qquad \delta_1(3) = 0.3 * 0.5 = 0.15$$ $$\delta_2(i) = \max \limits_{1 \le j \le n} ( \delta_1(j) a_{ji}) b_{i黑}$$ $$\delta_2(1) = max(\delta_1(1)*a_{11}, \delta_1(2)*a_{21}, \delta_1(3)*a_{31}) * b_{1黑} = max(0.08*0.5, 0.4*0.2, 0.15*0.2) * 0.6 = max(0.04, 0.08, 0.03) * 0.6 = 0.08*0.6 = 0.048$$ $$\delta_2(2) = max(\delta_1(1)*a_{12}, \delta_1(2)*a_{22}, \delta_1(3)*a_{32}) * b_{2黑} = max(0.08*0.4, 0.4*0.2, 0.15*0.5) * 0.2 = max(0.032, 0.08, 0.075) * 0.2 = 0.08*0.2 = 0.016$$ $$\delta_2(3) = max(\delta_1(1)*a_{13}, \delta_1(2)*a_{23}, \delta_1(3)*a_{33}) * b_{3黑} = max(0.08*0.1, 0.4*0.6, 0.15*0.3) * 0.5 = max(0.008, 0.24, 0.045) * 0.5 = 0.24*0.5 = 0.12$$ $$\delta_3(i) = \max \limits_{1 \le j \le n} ( \delta_2(j) a_{ji}) b_{i白}$$ $$\delta_3(1) = max(\delta_2(1)*a_{11}, \delta_2(2)*a_{21}, \delta_2(3)*a_{31}) * b_{1白} = max(0.048*0.5, 0.016*0.2, 0.12*0.2) * 0.4 = max(0.024, 0.0032, 0.024)*0.4 = 0.024*0.4 = 0.0096$$ $$\delta_3(2) = max(\delta_2(1)*a_{12}, \delta_2(2)*a_{22}, \delta_2(3)*a_{32}) * b_{2白} = max(0.048*0.4, 0.016*0.2, 0.12*0.5) * 0.8 = max(0.0192, 0.0032, 0.06)*0.8 = 0.06*0.8 = 0.048$$ $$\delta_3(3) = max(\delta_2(1)*a_{13}, \delta_2(2)*a_{23}, \delta_2(3)*a_{33}) * b_{3白} = max(0.048*0.1, 0.016*0.6, 0.12*0.3) * 0.5 = max(0.0048, 0.0096, 0.036)*0.5 = 0.036*0.5 = 0.018$$ $$\delta_4(i) = \max \limits_{1 \le j \le n} ( \delta_3(j) a_{ji}) b_{i白}$$ $$\delta_4(1) = max(\delta_3(1)*a_{11}, \delta_3(2)*a_{21}, \delta_3(3)*a_{31}) * b_{1白} = max(0.0096*0.5, 0.048*0.2, 0.018*0.2)*0.4 = max(0.0048, 0.0096, 0.0036)*0.4 = 0.0096*0.4 = 0.00384$$ $$\delta_4(2) = max(\delta_3(1)*a_{12}, \delta_3(2)*a_{22}, \delta_3(3)*a_{32}) * b_{2白} = max(0.0096*0.4, 0.048*0.2, 0.018*0.5)*0.8 = max(0.00384, 0.0096, 0.009)*0.8 = 0.0096*0.8 = 0.00768$$ $$\delta_4(3) = max(\delta_3(1)*a_{13}, \delta_3(2)*a_{23}, \delta_3(3)*a_{33}) * b_{3白} = max(0.0096*0.1, 0.048*0.6, 0.018*0.3)*0.5 = max(0.00096, 0.0288, 0.0054)*0.5 = 0.0288*0.5 = 0.0144$$ $$\delta_5(i) = \max \limits_{1 \le j \le n} ( \delta_4(j) a_{ji}) b_{i黑}$$ $$\delta_5(1) = max(\delta_4(1)*a_{11}, \delta_4(2)*a_{21}, \delta_4(3)*a_{31}) * b_{1黑} = max(0.00384*0.5, 0.00768*0.2, 0.0144*0.2 )*0.6 = max(0.00192, 0.001536, 0.00288)*0.6 = 0.00288*0.6 = 0.001728$$ $$\delta_5(2) = max(\delta_4(1)*a_{12}, \delta_4(2)*a_{22}, \delta_4(3)*a_{32}) * b_{2黑} = max(0.00384*0.4, 0.00768*0.2, 0.0144*0.5 )*0.2 = max(0.001536, 0.001536, 0.0072)*0.2 = 0.0072*0.2 = 0.00144$$ $$\delta_5(3) = max(\delta_4(1)*a_{13}, \delta_4(2)*a_{23}, \delta_4(3)*a_{33}) * b_{3黑} = max(0.00384*0.1, 0.00768*0.6, 0.0144*0.3 )*0.5 = max(0.000384, 0.004608, 0.00432)*0.5 = 0.004608*0.5 = 0.002304$$

同样的方法继续计算$\delta_3(i), \delta_4(i), \delta_5(i)$, 得到如下:

$$\delta_3(1)=0.0096, \delta_3(2)=0.048, \delta_3(3)=0.018$$ $$\delta_4(1)=0.00384, \delta_4(2)=0.00768, \delta_4(3)=0.0144$$ $$\delta_5(1)=0.001728, \delta_5(2)=0.00144, \delta_5(3)=0.002304$$

从$\delta_5$得知, $\delta_5(3)$最大, 往前推导, 第5个状态是由$\delta_4$的哪个产生的?
由$max(0.00384 \ast 0.1, 0.00768 \ast 0.6, 0.0144 \ast 0.3)$
得到是由$\delta_4(2)$来的, 依次往回倒推

5 -> 4 -> 3 -> 2 -> 1
3 -> 2 -> 2 -> 3 -> 2

可以看出盒子的序列为(2, 3, 2, 2, 3)

参考
盒子顺序的正确解释