precision和accuracy的区别

confusion matrix

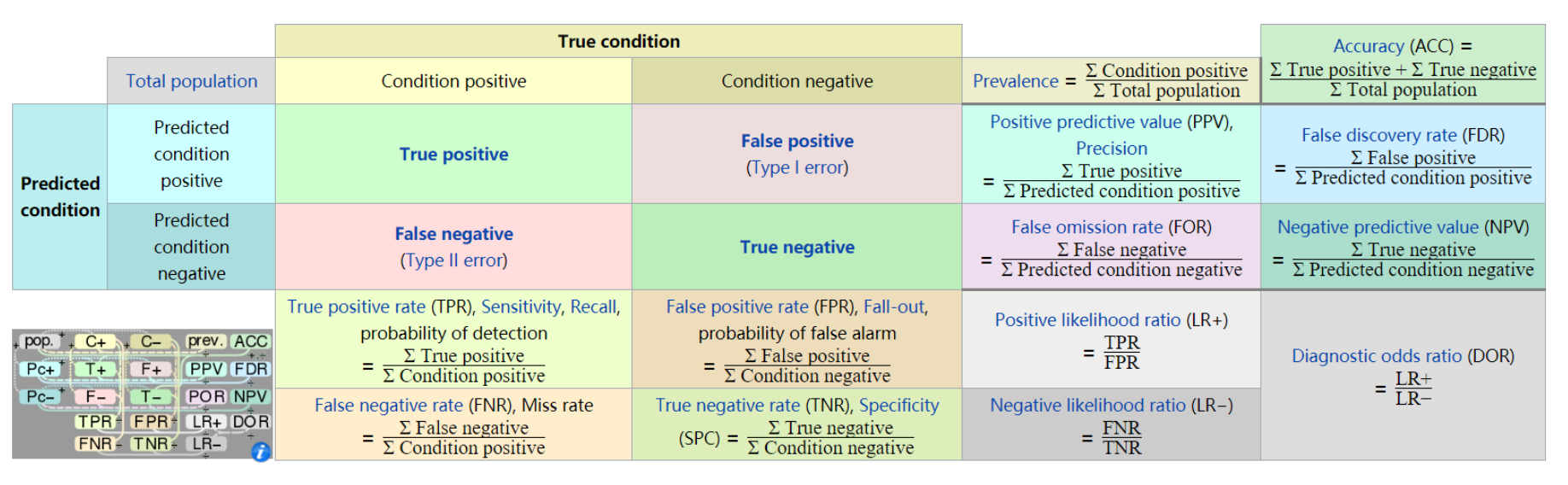
True positive(TP), 真正例, 被正确的划分为正例的个数, 即实际为正例且被分类器划分为正例的实例数/样本数
True negative(TN), 真负例, 被正确的划分为负例的个数, 即实际为负例且被分类器划分为负例的实例数
False positive(FP), 假正例, 被错误的划分为正例的个数, 即实际为负例且被分类器划分为正例的实例数
False negative(FN), 假负例, 被错误的划分为负例的个数, 即实际为正例且被分类器划分为负例的实例数
参考

实际值为正例的是True positive(TP)和False negative(FN)
实际值为负例的是True negative(TN)和False positive(FP)
预测值为正例的是True positive(TP)和False positive(FP)
预测值为负例的是True negative(TN)和False negative(FN)

		预测值	预测值
		正例	负例
实际值	正例	true positive(TP)真正例	false negative(FN)假负例
实际值	负例	false positive(FP)假正例	true negative(TN)真负例

还可以用如下的方式进行理解
正例记为+1, 负例记为-1, true用+1表示, false用-1表示, 那么

$$True positive(TP) = 1 * 1 = 1, 实际值为正例$$ $$True negative(TN) = 1 * (-1) = -1, 实际值为负例$$ $$False positive(FP) = (-1) * 1 = -1, 实际值为负例$$ $$False negative(FN) = (-1) * (-1) = 1, 实际值为正例$$

difference between accuracy and precision

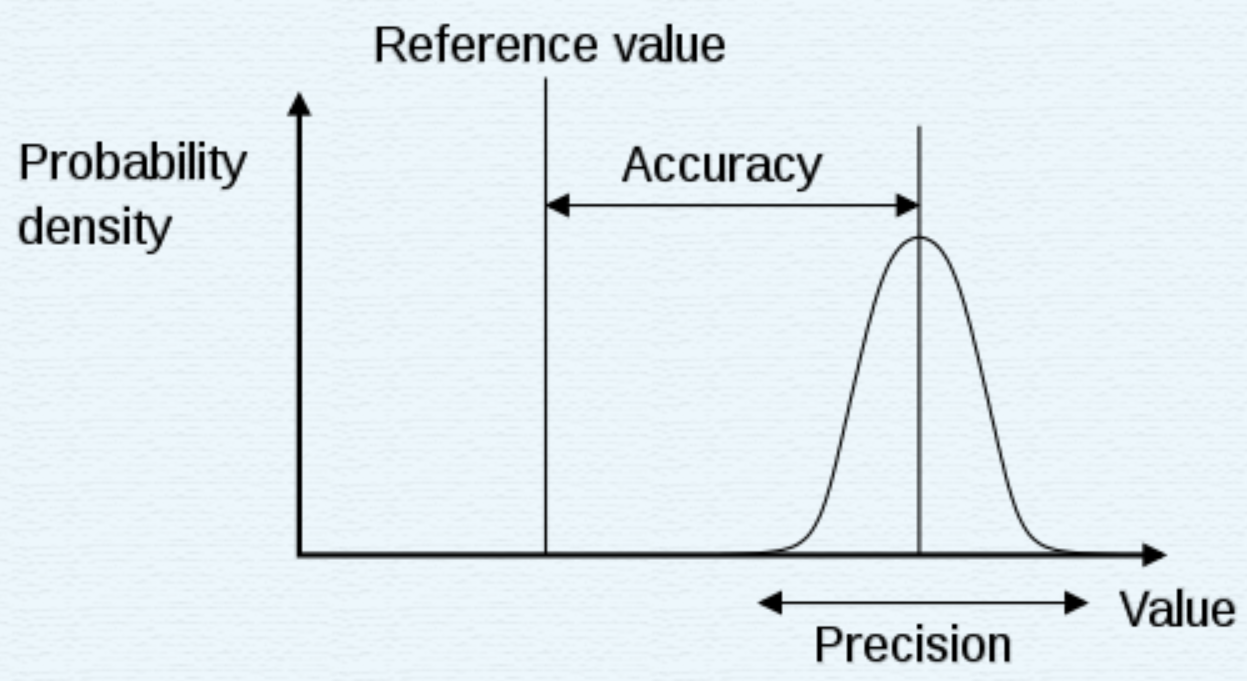
In the fields of engineering, industry and statistics, the accuracy of a measurement system is the degree of closeness of measurements of aquantity to its actual (true) value. The precision of a measurement system, also called reproducibility or repeatability, is the degree to which repeated measurements under unchanged conditions show the same results.[1] Although the two words can be synonymous in colloquial use, they are deliberately contrasted in the context of the scientific method.

Accuracy(准确度), is the difference between the measured value and the true value of a tested material.
Precision(精确度), is the repeatability of successive measurements under the same conditions.

Accuracy is how close a measured value is to the actual(true) value.
Precision is how close the measured values are to each other.

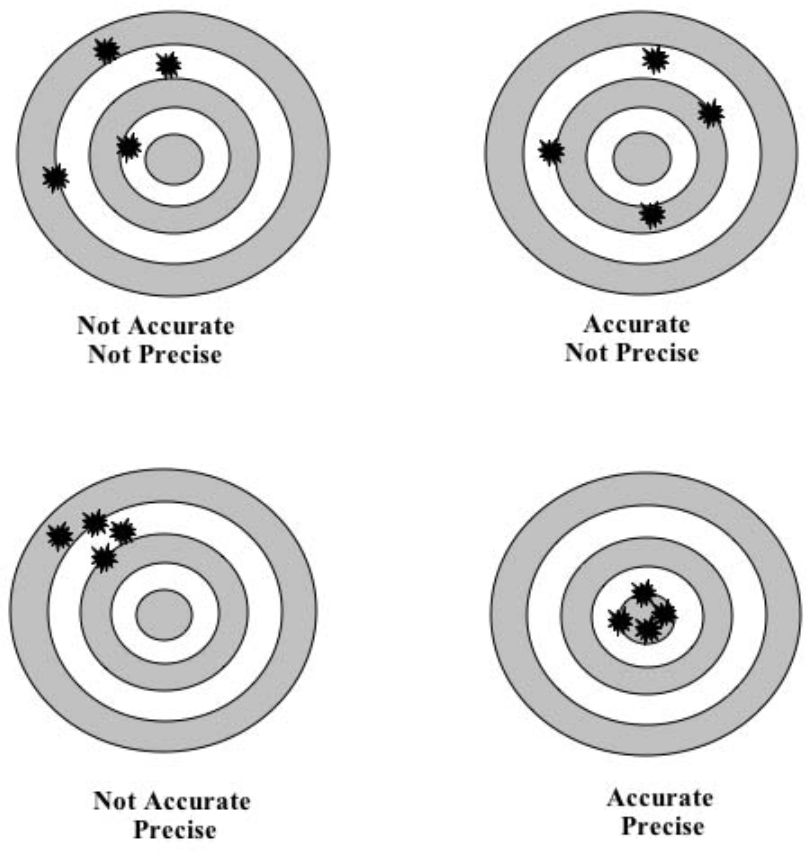
Accuracy, 指在一定实验条件下多次测试的平均值和真实值相符合的程度, 以误差表示
Precision, 指多次重复测试同一量时各测定值之间彼此相符合的程度, 表征测定过程中随机误差的大小

Accuracy = 被正确划分的样本/所有预测的样本 =(TP + TN) / (TP + FP + TN + FN), 通常来说, 正确率越高, 分类器越好
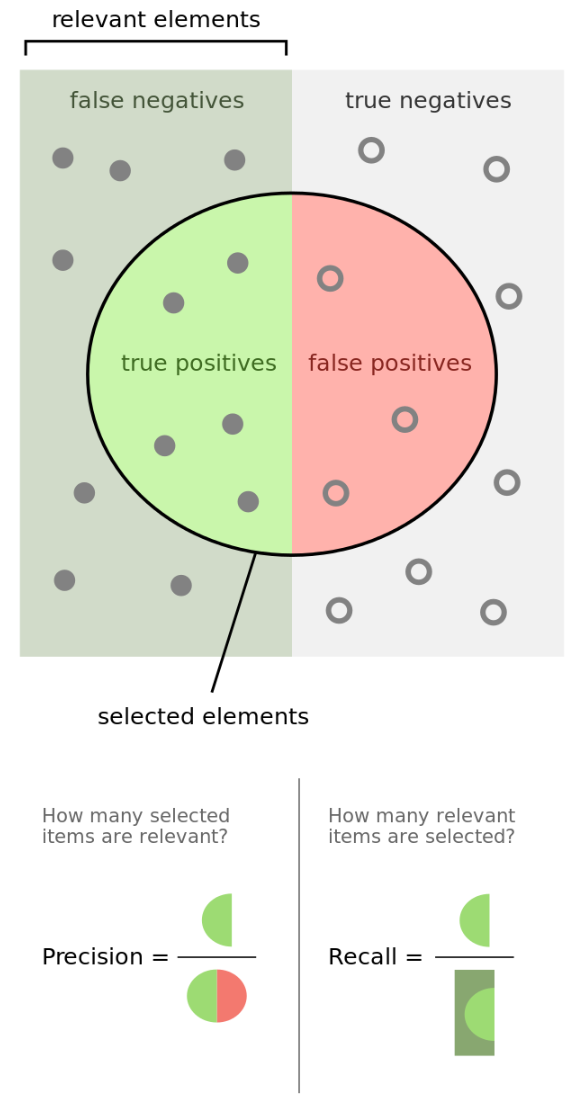
Precision = 真正例/预测为正例的样本 = TP / (TP + FP), 实际值为正例的样本占预测值为正例的比例
recall = 真正例/实际值为正例 = TP / (TP + FN), 召回率是覆盖面的度量, 实际值为正例的样本占实际值的比例, 召回率也叫做查全率

$$\displaystyle Precision = \frac{TP}{TP+FP} = \frac{正确被检索为正例的数量}{被检索为正例的数量}$$

用来描述被检索为正例的数量有多少是被正确检索的

$$\displaystyle Recall = \frac{TP}{TP+FN} = \frac{正确被检索为正例的数量}{应该被检索为正例的数量}$$

用来描述所有希望被检索的正例对象有多少被检索到了

理解precision和recall的另外一种角度

ROC, AUC和F-measure

ROC(Receiver Operating Characteristic), 受试者工作特征曲线, 在于曲线上各点反映着相同的感受性, 都是对同一信号刺激的反应, 只不过是在几种不同判定标准下得到的结果而已.
ROC反映了敏感性和特异性连续变量的综合指标, 用构图法揭示敏感性和特异性之间的相互关系, 通过将连续变量设定出多个不同的临界值, 从而计算出一系列敏感性和特异性, 再以敏感性为纵坐标, (1-特异性)为横坐标

$$TPR = TP/(TP+FN) = recall = sensitivity$$ $$FPR = FP/(FP+TN)$$ $$TNR = TN/(FP+TN) = specificity = 1 - FPR$$

纵轴是TPR(True Positive Rate), 横轴是1 - FPR(False Positive Rate)

AUC是ROC曲线下面积(Area Under roc Curve)的简称, 顾名思义, AUC的值就是处于ROC curve下方的那部分面积的大小. 通常, AUC的值介于0.5到1.0之间, AUC越大, 诊断准确性越高. 在ROC曲线上, 最靠近坐标图左上方的点为敏感性和特异性均较高的临界值.

Measuring Object Detection models - mAP - What is Mean Average Precision?

$$\displaystyle F = \frac{Precision \ast Recall \ast 2}{Precision + Recall}$$

补充

练习1

y_pred = [0, 1, 0, 0]
y_true = [0, 1, 0, 1]

真实值中a=2个1, b=2个0
预测值中c=1个1, d=3个0

TP = a - c = 1
TN = b = 2
FP = 0
FN = d - b = 1

		True condition	True condition
	Total population	Condition positive	Condition negative
Predicted condition	Predicted condition positive	TP=1	FP=0
Predicted condition	Predicted condition negative	FN=1	TN=2

precision = TP/(TP+FP) = 1/1 = 1
recall = TP/(TP+FN) = 1/(1+1) = 0.5
acc = (TP+TN)/(TP+TN+FP+FN) = (1+2)/(1+1+2)=0.75

上面是手算的结果

直接用程序如下:

from sklearn import metrics

y_pred = [0, 1, 0, 0]
y_true = [0, 1, 0, 1]

accuracy_score = metrics.accuracy_score(y_true, y_pred)
recall_score = metrics.recall_score(y_true, y_pred)
precision_score = metrics.precision_score(y_true, y_pred)

print(accuracy_score)
print(precision_score)
print(recall_score)

练习2

假如某个班级有男生80人,女生20人,共计100人.目标是找出所有女生.
现在某人挑选出50个人,其中20人是女生,另外还错误的把30个男生也当作女生挑选出来了.
作为评估者的你需要来评估(evaluation)下他的工作

真实值中, 被正确的分为女生的为TP=20, 被正确的分为男生的为TN=50
预测值中, 被错误的分为女生的为FP=30, 被错误的分为男生的为FN=0

		True condition	True condition
		condition positive	condition negative
Predicted condition	Predicted condition positive	TP=20	FP=30
Predicted condition	Predicted condition negative	FN=0	TN=50

precision = TP/(TP+FP) = 20/(20+30) = 0.4
recall = TP/(TP+FN) = 20/(20+0) = 1
acc = (TP+TN)/(all) = (20+50)/(100) = 0.7
F1_measure = (0.412)/(0.4+1) = 0.5714

例子

练习3

假设一个班级有100个学生，其中男生70人，女生30人。不知道这些学生的性别，只知道他们的身高和体重。我们有一个程序(分类器)，这个程序可以通过分析每个学生的身高和体重，对这100个学生的性别分别进行预测。最后的预测结果为，60人为男生，40人为女生

有两种方法来区分

第一种方法

设正例为男生, 那么负例就是女生
TP真正例, 实际值为男生, 预测值为男生
TN真负例, 实际值为女生, 预测值为女生
FP假正例, 实际值为女生, 预测值为男生
FN假负例, 实际值为男生, 预测值为女生

TP + FN = 70
TN + FP = 30
TP + FP = 60
TN + FN = 40

计算过程如下
TP, TN, FP, FN
1, 0, 0, 1, 70
0, 1, 0, 1, 40
0, 0, 1, -1, -10
0, 0, 0, 0, 0

FN - FP = 10

当FP=20, FN=30, TN=10, TP=40
acc = (TP+TN)/all = 50/100
precision = TP/(TP+FP) = 40/60
recall = TP/(TP+FN) = 40/70

当FP=10, FN=20, TN=20, TP=50
acc = (TP+TN)/all = 70/100
precision = TP/(TP+FP) = 50/60
recall = TP/(TP+FN) = 50/70

第二种方法

设正例为女生, 那么负例就是男生
TP真正例, 实际值为女生, 预测值为女生
TN真负例, 实际值为男生, 预测值为男生
FP假正例, 实际值为男生, 预测值为女生
FN假负例, 实际值为女生, 预测值为男生

TN+FP=70
TP+FN=30
TN+FN=60
TP+FP=40

TP TN FP FN b
0 1 1 0 70
1 0 0 1 30
0 1 0 1 60
1 0 1 0 40

1 0 0 1 30
1 0 1 0 40
0 1 1 0 70
0 1 0 1 60

1 0 0 1 30
0 1 1 0 70
0 0 1 -1 10
0 0 0 0 0

TP TN FP FN b
1 0 0 1 30
0 1 0 1 60
0 0 1 -1 10
0 0 0 0 0

TP=30-FN
TN=60-FN
FP=10+FN

令FN=10, TP=20, TN=50, FP=20
acc = (TP+TN)/all = 70/100
precision = TP/(TP+FP) = 20/40
recall = TP/(TP+FN) = 20/30

令FN=20, TP=10, TN=40, FP=30
acc = (TP+TN)/all = 50/100
precision = TP/(TP+FP) = 10/40
recall = TP/(TP+FN) = 10/30