数学概念

数学基础

常见函数

• 导数, 梯度
• Taylor展开, Taylor公式
• 概率论, 联合概率, 条件概率, 全概率公式, 贝叶斯公式
• 期望, 方差, 协方差
• 大数定理, 中心极限定理
• 估计法, 最大似然估计(MLE)
• 向量, 矩阵运算, 矩阵求导
• SVD, QR分解

梯度

梯度是一个向量, 表示某一个函数在该点处的方向导数沿着该方向取的最大值, 即函数在该点处沿着该方向变化最快, 变化率最大(即该梯度向量的模); 当函数为一维函数时, 梯度其实就是导数

$$\nabla{f(x_1, x_2)} = (\frac{\partial{f(x_1, x_2)}}{x_1}, \frac{\partial{f(x_1, x_2)}}{x_2})$$

Taylor公式

• Taylor公式是用一个函数在某点的信息描述其附近取值的公式. 如果函数足够平滑, 在已知函数在某一点的各阶导数值的情况下, Taylor公式可以利用这些导数值来做系数构建一个多项式近似函数在这一点的领域中的值.
• 若函数$f(x)$在包含$x_0$的某个闭区间$[a, b]$上具有$n$阶函数, 且在开区间$(a, b)$上具有$n+1$阶函数, 则对闭区间$[a, b]$上任意一点$x$, 有Taylor公式如下: $$f(x) = \frac{f(x_0)}{0!} + \frac{f^{'}(x_0)}{1!}(x-x_0) + \frac{f^{''}(x_0)}{2!}(x-x_0)^2 + ... + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n + R_n(x)$$

$f^{(n)}(x)$表示$f(x)$的$n$阶导数, $R_n(x)$是Taylor公式的余项, 是$(x-x_0)^n$的高阶无穷小

$$sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} + ... + (-1)^{m-1}\frac{x^{2m-1}}{(2m-1)!} + R_{2m-1}(x)$$

计算近似值, 并估计误差值

$$e = \lim_{x \rightarrow \infty}(1 + {\frac{1}{n})}^n$$ $$y = e^x \Rightarrow y^{'} = y = e^x$$ $$\begin{align} e^x &\approx \sum_{k=0}^{n}{\frac{e^x_0}{k!}}(x-x_0)^k\\ &\stackrel{令x_0=0}{\Rightarrow} e^x \approx 1 + x + \frac{x^2}{2!} + ... + \frac{x_n}{n!}\\ &\stackrel{令x=1}{\Rightarrow} e \approx 1 + 1 + \frac{1}{2!} + \frac{1}{3!} + ... + \frac{1}{n!}\\ &\stackrel{令x=10}{\Rightarrow} e \approx 2.7182815\\ \end{align}$$ $$\delta = \vert R_{10}\vert = \frac{1}{11!} + \frac{1}{12!} + ... = \frac{1}{11!}(1+\frac{1}{12}+\frac{1}{12*13}+...) \lt \frac{1}{11!}(1+\frac{1}{12}+\frac{1}{12^2}+...) = \frac{12}{11*11!} = 2.73 * 10^{-8}$$

联合概率

两个事件同时发生的概率, 计作: $P(AB)$, $P(A, B)$, 或者$P(A \cap B)$, 即为”事件A和事件B同时发生的概率”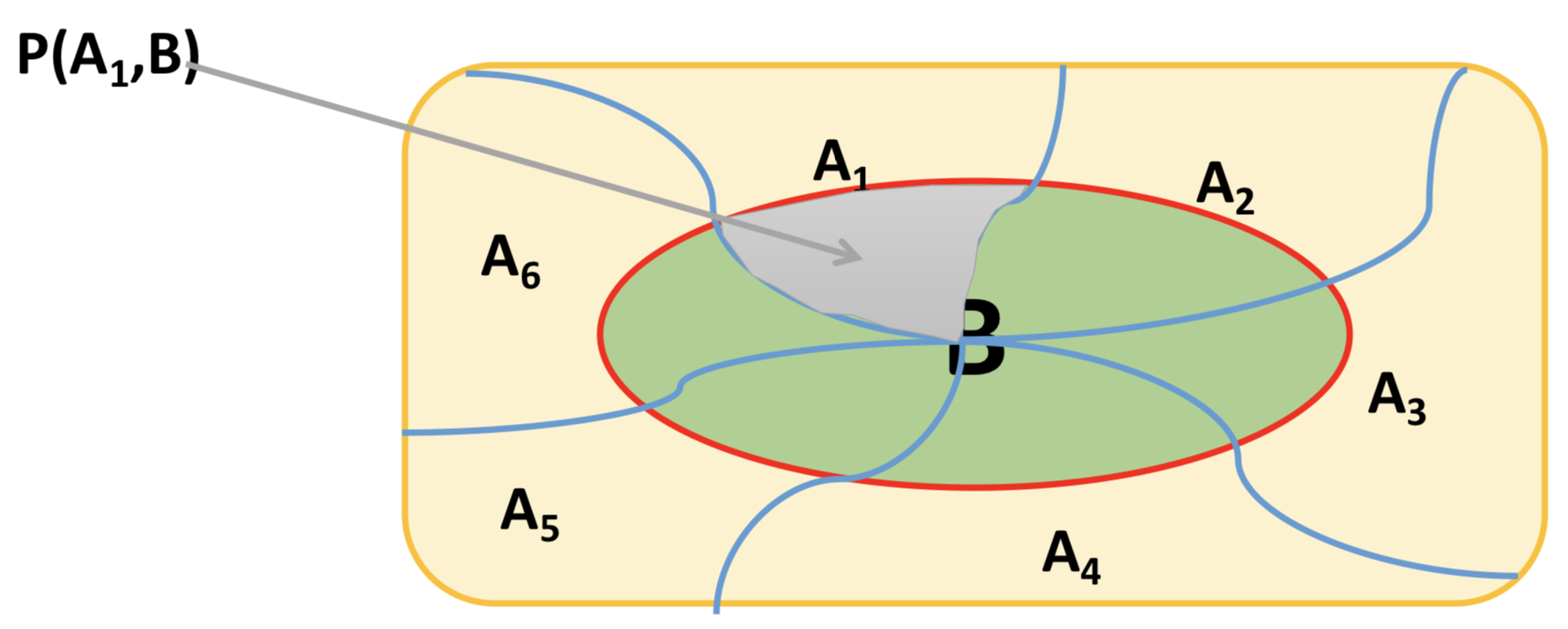

条件概率

事件A在另外一件事情B已经发生的条件下发生的概率叫做条件概率, 表示为P(A|B), 即为”在B条件下A发生的概率”
一般情况下, P(A|B) ≠ P(A)
条件概率有如下三个特性

• 非负性
• 可列性
• 可加性

$$P(A_1|B) = \frac{P(A_1, B)}{P(B)}$$

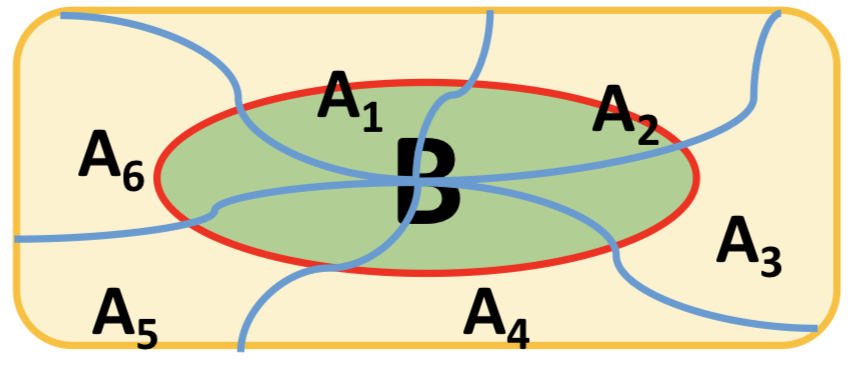
如果将条件概率由两个事件推广到任意有穷多个事件时, 可以得到如下公式, 假设$A_1, A_2, …, A_n$为任意n个任意事件(n ≥ 2)), 而且$P(A_1A_2…A_n) > 0$, 则

$$P(A_1B) = P(A_1|B)P(B)$$ $$P(A_1A_2) = P(A_1|A_2)P(A_2) = P(A_2)P(A_1|A_2)$$

即为, 事件$A_1$和事件$A_2$同时发生的概率等于事件$A_2$已经发生的条件下$A_1$发生的概率与事件$A_2$发生的概率的乘积

$$P(A_2A_1) = P(A_2|A_1)P(A_1) = P(A_1)P(A_2|A_1)$$

即为, 事件$A_2$和事件$A_1$同时发生的概率等于事件$A_1$已经发生的条件下$A_2$发生的概率与事件$A_1$发生的概率的乘积

$$P(A_1A_2) = P(A_2, A_1)$$

即为, 事件$A_1$和事件$A_2$同时发生的概率

$$P(A_1|A_2)P(A_2) = P(A_2|A_1)P(A_1)$$

即为, 事件$A_2$已经发生的条件下$A_1$发生的概率与事件$A_2$发生的概率的乘积 等于 事件$A_1$已经发生的条件下$A_2$发生的概率与事件$A_1$发生的概率的乘积

$$P(A_1A_2A_3) = P(A_1A_2)P(A_3|(A_1A_2)) = P(A_1)P(A_2|A_1)P(A_3|(A_1A_2))$$ $$P(A_1A_2...A_n) = P(A_1)P(A_2|A_1)...P(A_n|(A_1A_2...A_n))$$

全概率

样本空间$\Omega$有一组事件$A_1, A_2, …, A_n$, 如果事件组满足以下两个条件, 那么事件组称为样本空间的一个划分:

• $\forall i ≠ j \in \{1, 2, …, n\}, A_iA_j = \phi$
• $A_1 \cup A_2… \cup A_n = \Omega$

如果事件$\{A_j\}$是样本空间$\Omega$的一个划分, 且$P(A_j) > 0$, 那么对于任意事件B, 全概率公式为:

$$P(B) = \sum_{i=1}^{n}{P(A_i)P(B|A_i)}$$

贝叶斯公式

$$P(A|B) = \frac{P(B|A)P(A)}{P(B)}$$

设$A_1, A_2, …, A_n$是样本空间$\Omega$的一个划分, 如果对于任意事件B, 有$P(B) > 0$, 那么

$$P(A_i|B) = \frac{P(B|A_i)P(A_i)}{P(B)} = \frac{P(A_i)P(B|A_i)}{\displaystyle \sum_{i=1}^{n}{P(A_i)P(B|A_i)}}$$

概率公式总结

$$P(A|B) = \frac{P(A, B)}{P(B)}$$ $$P(B) = \sum_{i=1}^{n}{P(A_i)P(B|A_i)}$$ $$P(A_i|B) = \frac{P(A_i, B)}{P(B)}$$ $$P(A_i|B) = \frac {P(A_i)P(B|A_i)} {\displaystyle \sum_{i=1}^{n}{P(A_i)P(B|A_i)} }$$

期望

期望即均值, 是概率加权下的”平均值”, 是每次可能结果的概率乘以其结果的总和, 反映的是随机变量平均取值大小, 常用符号$\mu$表示:

• 连续性数据, $E(X) = \int_{-\infty}^{+\infty}xf(x)dx$
• 离散性数据, $E(X) = \sum_{i}{x_ip_i}$

假设C为一个常数, X和Y是两个随机变量, 期望的性质如下:

• E(C) = C
• E(CX) = CE(X)
• E(X + Y) = E(X) + E(Y)
• 如果X和Y相互独立, 那么E(XY) = E(X)E(Y)
• 如果E(XY) = E(X)E(Y), 那么X和Y不相关

方差

衡量随机变量或一组数据离散程度的度量, 是用来度量随机变量和其数学期望之间的偏离程度. 即方差是衡量原数据和期望/均值相差的度量值.

$$Var(X) = D(X) = \sigma^2 = \frac{\sum{(X-\mu)^2}}{N}$$ $$D(X) = \sum_{n=1}^{n}{P_i}{(X_i-\mu)^2}$$ $$D(X) = \int_a^b(x-u)^2f(x)dx$$ $$D(X) = E((X-E(X))^2) = E(X^2) - (E(x))^2$$

X	2	4	6	8	10
$P(x)$	0.2	0.2	0.2	0.2	0.2

$$E(X) = 2*0.2 + 4*0.2 + 6*0.2 + 8*0.2 + 10*0.2 = 6$$ $$\begin{align} E(X^2) &= 2^2*0.2 + 4^2*0.2 + 6^2*0.2 + 8^2*0.2 + 10^2*0.2\\ &= 4*0.2 + 16*0.2 + 36*0.2 + 64*0.2 + 100*0.2\\ &= 220*0.2\\ &= 44 \end{align}$$ $$D(X) = E(X^2) - (E(X))^2 = 44 - 6^2 = 8$$

假设C是一个常数, X和Y是两个随机变量, 那么方差的性质如下:

$D(C) = 0$
$D(CX) = C^2D(X)$
$D(C + X) = D(X)$
$D(X \pm Y) = D(X) + D(Y) \pm 2 Cov(X,Y)$

标准差

标准差(Standard Deviation)是方差的算术平方根, 用符号$\sigma$表示.
标准差和方差都是测量离散程度最重要最常见的指标. 不同之处在于标准差和变量的计算单位是相同的, 比方差清楚, 因此在很多分析的时候用标准差.

$$\sigma = \sqrt{D(X)} = \sqrt{\frac{\sum(X-\mu)^2}{N}}$$

协方差

协方差常用于衡量两个变量的总体误差, 当两个变量相同的情况下, 协方差其实就是方差
如果X和Y是统计独立的, 那么二者之间的协方差为零; 如果协方差为零, 那么X和Y是不相关的.

$$\begin{align} Cov(X,Y) &= E[(X-E(X))(Y-E(Y))]\\ &= E[XY - XE(Y) - YE(X) + E(X)E(Y)]\\ &= E(XY) - E(X)E(Y) - E(Y)E(X) + E(X)E(Y)\\ &= E(XY) - E(X)E(Y)\\ \end{align}$$

假设C为一个常数, X和Y是两个随机变量, 那么协方差性质如下:

$$Cov(X, Y) = Cov(Y, X)$$ $$Cov(aX, bY) = abCov(X, Y)$$ $$Cov(X_1 + X_2, Y) = Cov(X_1, Y) + Cov(X_2, Y)$$

协方差是两个随机变量具有相同方向变化趋势的度量:

• 若$Cov(X, Y) > 0$, 则X和Y的变化趋势相同
• 若$Cov(X, Y) < 0$, 则X和Y的变化趋势相反
• 若$Cov(X, Y) = 0$, 则X和Y则不相关, 即变化没有什么相关性

对于n个随机向量($X_1, X_2, X_3…X_n$), 任意两个元素$X_i$和$X_j$都可以得到一个协方差, 从而形成一个n*n的矩阵即为协方差矩阵, 协方差矩阵为对称矩阵

$$C_{ij} = E\{[E_i - E(X_i)][E_j - E(X_j)]\} = Cov(X_i, X_j)$$ $$\begin{bmatrix} {c_{11}}&{c_{12}}&{\cdots}&{c_{1n}}\\ {c_{21}}&{c_{22}}&{\cdots}&{c_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {c_{m1}}&{c_{m2}}&{\cdots}&{c_{mn}}\\ \end{bmatrix}$$

大数定律

• 大数定律的意义在于, 随着样本容量n的增加, 样本平均数将接近于总体平均数(期望$\mu$), 所以在统计推断中, 一般都会使用样本平均数估计总体平均数的值.
• 使用一部分样本的平均值来代替整体样本的期望/均值, 出现偏差的可能是存在的, 但是当n足够大的时候, 偏差的可能性是非常小的, 当n无限大的时候, 这种可能性的概率基本为0
• 大数定律的作用就是为使用频率来估计概率提供来理论支持; 为使用部分数据来近似的模拟构建全部数据特征提供来理论支持

中心极限定理

• 中心极限定理(Central Limit Theorem), 假设${X_n}$为独立同分布的随机变量序列, 并有相同的期望$\mu$和方差$\sigma^2$, 则$X_n$服从中心极限定理, 且${Z_n}$为随机序列${X_n}$的规范和: $$Y_n = X_1 + X_2 + ... + X_n = \sum_{n=1}^{n}{X_i} \rightarrow N(n\mu, n\sigma^2)$$ $$Z_n = \frac{Y_n - E(Y_n)}{\sqrt{D(Y_n)}} = \frac{Y_n - n\mu}{\sqrt{n}\sigma} \rightarrow(0, 1)$$
• 中心极限定理就是一般在同分布的情况下, 抽样样本值的规范和在总体数量趋于无穷时的极限分布近似于正态分布

最大似然估计

• 最大似然估计(Maximum Likelihood Estimation, MLE)是一种具有理论性的参数估计方法. 基本思想: 当从模型总体随机抽取n组样本观测值后, 最合理的参数估计量应该使得从模型中抽取n组样本观测值的概率最大, 步骤如下:
  • 写出似然函数
  • 对似然函数取对数, 并整理
  • 求导数
  • 解似然函数

设总体分布为$f(x, \theta)$, $X_n$为该总体采样得到的样本. 因为随机序列${X_n}$独立同分布, 则它们的联合密度函数为:

$$L(x_1, x_2, ..., x_n) = \prod_{i=1}^{n}{f(x_i; \theta_1, \theta_2, ..., \theta_n)}$$

• $\theta$被看作固定但是未知的参数, 反过来, 因为样本的已经存在, 可以看作${X_n}$是固定的, $L(x, \theta)$是关于$\theta$的函数, 即似然函数
• 求参数$\theta$, 使得似然函数取最大值, 此为最大似然估计法

似然与极大似然估计

向量的运算

两个向量: $\overrightarrow{a} = (x_1, y_1)$, $\overrightarrow{b} = (x_2, y_2)$, 并且a和b之间的夹角为$\theta$

• 数量积: 两个向量的数量积(内积, 点积)是一个数量/实数, 记作$\overrightarrow{a} \cdot \overrightarrow{b}$ $$\overrightarrow{a} \cdot \overrightarrow{b} = \vert \overrightarrow{a} \vert * \vert \overrightarrow{b} \vert * cos\theta$$
• 向量积: 两个向量的向量积(外积, 叉积)是一个向量, 记作$\overrightarrow{a} \times \overrightarrow{b}$; 向量积即两个不共线非零向量所在平面的一组法向量 $$\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert * \vert \overrightarrow{b} \vert * sin\theta$$

矩阵的运算

• 假设A, B均为$m*n$阶矩阵, 那么
  • $C = A \pm B$
  • $A + B = B +A$
  • $(A + B) + C = A + (B + C)$
  • $(\lambda\mu)A = \lambda(\mu A)$
  • $\lambda(A + B) = \lambda A + \lambda B$
  • $(AB)C = A(BC)$
  • $(A + B)C = AC + BC$
  • $C(A + B) = CA + CB$
  • $(A^T)^T = A$
  • $(\lambda A)^T = \lambda A^T$
  • $(AB)^T = B^TA^T$
  • $(A + B)^T = A^T + B^T$

QR分解

• QR分解是将矩阵分解为一个正交矩阵和一个上三角矩阵的乘积

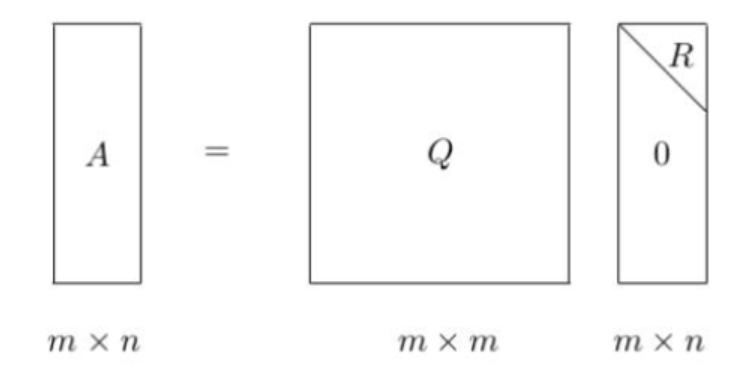
• 其中, Q为正交矩阵, $Q^TQ = I, R为上三角矩阵$
• QR分解经常被用来解线性最小二乘问题

SVD分解

• 奇异值分解(Singular Value Decomposition)是一种重要的矩阵分解方法, 可以看作是对称矩阵在任意矩阵上的推广
• 假设A为一个$m*n$阶的实矩阵, 则存在一个分解使得: $$A_{m*n} = U_{m*n}\Sigma_{m*n}V_{m*n}^T$$
  • 通常奇异值由大到小排列, 这样$\Sigma$便能由A唯一确定了

向量的导数

A为一个$m*n$阶的矩阵, $x$为$n\ast1$的列向量, 则$Ax$为$m\ast1$的列向量, 计作$\overrightarrow{y} = A \cdot \overrightarrow{x}$

$$A = \begin{bmatrix} {a_{11}}&{a_{12}}&{\cdots}&{a_{1n}}\\ {a_{21}}&{a_{22}}&{\cdots}&{a_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {a_{m1}}&{a_{m2}}&{\cdots}&{a_{mn}}\\ \end{bmatrix}$$ $$\overrightarrow{x} = \begin{bmatrix} {x_{1}}\\ {x_{2}}\\ {\vdots}\\ {a_{n}}\\ \end{bmatrix}$$ $$\overrightarrow{y} = \begin{bmatrix} {a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n}\\ {a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n}\\ {\vdots}\\ {a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n}\\ \end{bmatrix}$$ $$\frac{ \partial \overrightarrow{y} }{ \partial \overrightarrow{x} } = \frac{ \partial A\overrightarrow{x} }{ \partial \overrightarrow{x} } = \displaystyle \frac{\partial}{\partial \overrightarrow{x}} \begin{bmatrix} {a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n}\\ {a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n}\\ {\vdots}\\ {a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n}\\ \end{bmatrix} = \begin{bmatrix} {a_{11}}&{a_{21}}&{\cdots}&{a_{m1}}\\ {a_{12}}&{a_{22}}&{\cdots}&{a_{m2}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {a_{1n}}&{a_{2n}}&{\cdots}&{a_{mn}}\\ \end{bmatrix} = A^T$$

向量的导数

$$\frac{\partial A \overrightarrow{x}}{\partial \overrightarrow{x}} = A^T$$ $$\frac{\partial A \overrightarrow{x}}{\partial \overrightarrow{x}^T} = A$$ $$\frac{\partial (\overrightarrow{x}^TA)}{\partial \overrightarrow{x}} = A$$

标量对向量的导数

• $A$为$n*n$的矩阵, $x$为$n \ast 1$的列向量, 计作$\overrightarrow{y} = \overrightarrow{x}^T \cdot A \cdot \overrightarrow{x}$
• 同理可得: $$\frac{\partial{y}}{\partial{\overrightarrow{x}}} = \frac{\partial(\overrightarrow{x}^T \cdot A \cdot \overrightarrow{x})}{\partial{\overrightarrow{x}}} = (A^T + A) \cdot \overrightarrow{x}$$
• 若A为对称矩阵, 则有 $$\frac{\partial(\overrightarrow{x}^T A \overrightarrow{x})}{\partial{\overrightarrow{x}}} = 2A\overrightarrow{x}$$ 推导过程如下:

$$A = \begin{bmatrix} {a_{11}}&{a_{12}}&{\cdots}&{a_{1n}}\\ {a_{21}}&{a_{22}}&{\cdots}&{a_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {a_{m1}}&{a_{m2}}&{\cdots}&{a_{mn}}\\ \end{bmatrix}$$ $$\overrightarrow{x} = \begin{bmatrix} {x_{1}}\\ {x_{2}}\\ {\vdots}\\ {a_{n}}\\ \end{bmatrix}$$ $$\begin{align} \overrightarrow{x}^T A \overrightarrow{x} &= (x_1, x_2,\cdots, x_n) \begin{bmatrix} {a_{11}}&{a_{12}}&{\cdots}&{a_{1n}}\\ {a_{21}}&{a_{22}}&{\cdots}&{a_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {a_{n1}}&{a_{n2}}&{\cdots}&{a_{nn}}\\ \end{bmatrix} \begin{bmatrix} {x_{1}}\\ {x_{2}}\\ {\vdots}\\ {a_{n}}\\ \end{bmatrix}\\ &=(x_1, x_2,\cdots, x_n)(\Sigma_{j=1}^{n}{a_{1j}{x_j}}, \Sigma_{j=1}^{n}{a_{2j}{x_j}}, \cdots, \Sigma_{j=1}^{n}{a_{nj}{x_j}})^T\\ &=x_1\Sigma_{j=1}^{n}{a_{1j}{x_j}} + x_2\Sigma_{j=1}^{n}{a_{2j}{x_j}} + \cdots + x_n\Sigma_{j=1}^{n}{a_{nj}{x_j}}\\ &=\Sigma_{i=1}^{n} \Sigma_{j=1}^{n} a_{ij} x_i x_j\\ \end{align}$$ $$\begin{align} \frac{\partial(\overrightarrow{x}^T A \overrightarrow{x})}{\overrightarrow{x}} &= \frac{\partial(\Sigma_{i=1}^{n} \Sigma_{j=1}^{n} a_{ij} x_i x_j)}{\overrightarrow{x}}\\ &=\frac{\partial}{\overrightarrow{x}}[\Sigma_{i=1}^{n}(a_{i1}x_ix_1 + a_{i2}x_ix_2 + \cdots + a_{in}x_ix_n)]\\ &= \frac{\partial}{\overrightarrow{x}}[\\ &a_{11}x_1x_1 + a_{12}x_1x_2 + \cdots + a_{1n}x_1x_n +\\ &a_{21}x_2x_1 + a_{22}x_2x_2 + \cdots + a_{2n}x_2x_n +\\ &\vdots\\ &a_{n1}x_nx_1 + a_{n2}x_nx_2 + \cdots + a_{nn}x_nx_n ]\\ &=\\ &[a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n +\\ &a_{21}x_2+\\ &\vdots\\ &a_{n1}x_n] +\\ [&\qquad\quad a_{12}x_1 +\\ &a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n +\\ &\vdots\\ &\qquad\quad a_{n2}x_n] +\\ & \vdots\\ &+ \\ [&\qquad \qquad \qquad \qquad \qquad a_{1n}x_1 +\\ &\qquad \qquad \qquad \qquad \qquad a_{2n}x_2 +\\ &\vdots\\ &+ \\ &a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nn}x_n]\\ \end{align}$$

由上式得到

$$\begin{bmatrix} {2a_{11}}&{a_{12}}&{a_{13}}&{\cdots}&{a_{1n}}\\ {a_{21}}&{0}&{0}&{\cdots}&{0}\\ {a_{31}}&{0}&{0}&{\cdots}&{0}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {a_{m1}}&{0}&{0}&{\cdots}&{0}\\ \end{bmatrix} + \begin{bmatrix} {0}&{a_{12}}&{0}&{\cdots}&{0}\\ {a_{21}}&{2a_{22}}&{a_{23}}&{\cdots}&{a_{2n}}\\ {0}&{a_{32}}&{0}&{\cdots}&{0}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {0}&{a_{n2}}&{0}&{\cdots}&{0}\\ \end{bmatrix} + \cdots + \begin{bmatrix} {0}&{0}&{0}&{\cdots}&{a_{1n}}\\ {0}&{0}&{0}&{\cdots}&{a_{2n}}\\ {0}&{0}&{0}&{\cdots}&{a_{3n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {a_{m1}}&{a_{m2}}&{a_{m3}}&{\cdots}&{2a_{mn}}\\ \end{bmatrix} = \Sigma_{j=1}^{n}(a_{ij} + a_{ji})x_j$$

标量对方阵对导数

A为$n * n$的矩阵, $|A|$为A的行列式, 计算$\frac{\partial{|A|}}{\partial{A}}$

$$\forall 1 \le i \le n, |A| = \Sigma_{j=1}^{n}a_{ij}(-1)^{i+j}M_{ij}$$ $$\frac{\partial |A|}{\partial a_{ij}} = \frac{\partial(\Sigma_{j=1}^{n}a_{ij}(-1)^{i+j}M_{ij})}{\partial a_{ij}} = (-1)^{i+j}M_{ij} = A_{ji}^*$$ $$\frac{\partial \lvert A \rvert}{\partial A} = (A^*)^T = \lvert A \rvert \cdot (A^{-1})^T$$

模型训练及测试

• 模型选择, 对特定任务最优建模方法的选择或者对特定模型最佳参数的选择
• 在训练数据集上运行模型(算法)并在测试数据集中测试效果, 迭代进行数据模型对修改, 这种方式称为交叉验证(将原始数据分为训练集和测试集, 使用训练集构建模型, 并使用测试集评估模型提供修改意见)
• 模型的选择会尽可能多的选择算法进行执行, 并比较执行结果
• 模型的测试一般从以下几个方面来进行比较, 分别是准确率, 召回率, 精准率, F值
  • 准确率(Accuracy) = 提取出的正确样本数/总样本数
  • 召回率(Recall) = 正确的正例样本数/样本中的正例样本数- 覆盖率
  • 精确度(Precision) = 正确的正例样本数/预测为正例的样本数
  • F值 = Precision Recall 2 / (Precision + Recall), 即F值是精准度和召回率的调和平均值

		预测值
		正例	负例
真实值	正例	true positive真正例(A)	false negative假负例(B)
	负例	false positive假正例(C)	true negative真负例(D)

true positive(hit)真正例, 确实是正例
true negative(Correct Rejection)真负例, 确实是负例
false positive(False Alarm)假正例, 本来真实值是负例, 被预测为正例了, 虚报, 干扰报警
false negative(Miss)假负例, 本来真实值是正例, 被预测为负例了, 即没有预测出来

击中(Hit)(报准)和正确拒绝(Correct Rejection)是正确反应, 虚报(False Alarm)和漏报(Miss)是错误反应

A和D预测正确, B和C预测错误, 那么计算结果为:

$$Accuracy = (A + D) / (A + B + C + D)$$ $$Recall = A / (A + B)$$ $$Precision = A / (A + C)$$ $$\displaystyle F = \frac{Precision \ast Recall \ast 2}{Precision + Recall}$$

举个例子, 真实值中, 正例为80, 负例为20; 预测值中, 正例为90, 负例为10, 然而, 在模型的实际预测中, 原本有75个真正的正例, 有15个是假正例, 5个假负例和5个真负例, 如下图所示:

		预测值
		正例90	负例10
真实值	正例80	真正例(A)75	假负例(B)5
	负例20	假正例(C)15	真负例(D)5

Accuracy和Recall是一对互斥的关系, Accuracy在增大的时候Recall是在减小的

precision和accuracy的区别

ROC

ROC(Receiver Operating Characteristic), 描述的是分类混淆矩阵中FPR-TPR之间的相对变化情况.
纵轴是TPR(True Positive Rate), 横轴是FPR(False Positive Rate)

如果二元分类器输出的是对正样本对一个分类概率值, 当取不同阈值时会得到不同当混淆矩阵， 对应于ROC曲线上当一个点, ROC曲线就反应了FPR和TPR之间权衡当情况, 通俗的说, 即在TPR随着FPR递增的情况下, 谁增长的更快, 快多少的问题. TPR增长的越快, 曲线越往上弯曲, AUC就越大, 反应了模型的分类性能就越好. 当正负样本不平衡时, 这种模型评价方式比起一般当精确度评价方式的好处尤其显著.

AUC(Area Under Curve)

AUC被定义为ROC曲线下的面积, 显然这个面积的数值不会大于1. 由于ROC曲线一般都处于y=x这条直线的上方, 所以AUC的取之范围在0.5和1之间. AUC作为数值可以直观的评价分类器的好坏, 值越大越好.

AUC的值一般要求在0.7以上.

模型评估

回归结果度量

• explained_varicance_score, 可解释方差的回归评分函数
• mean_absolute_error, 平均绝对误差
• mean_squared_error, 平均平方误差

模型评估总结_分类算法评估方式

指标	描述	scikit-learn函数
Precision	精确度	from sklearn.metrics import precision_score
Recall	召回率	from sklearn.metrics import recall_score
F1	F1指标	from sklearn.metrics import f1_score
Confusion Matrix	混淆矩阵	from sklearn.metrics import confusion_matrix
ROC	ROC曲线	from sklearn.metrics import roc
AUC	ROC曲线下的面积	from sklearn.metrics import auc
Mean Square Error(MSE, RMSE)	平均方差	from sklearn.metrics import mean_squared_error
Absolute Error(MAE, RAE)	平均方差	from sklearn.metrics import mean_absolute_error, median_absolute_error
R-Squared	平均方差	from sklearn.metrics import r2_score

$$\overrightarrow{x}^T A \overrightarrow{x} = (x_1, x_2,\cdots, x_n) \begin{bmatrix} {a_{11}}&{a_{12}}&{\cdots}&{a_{1n}}\\ {a_{21}}&{a_{22}}&{\cdots}&{a_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {a_{n1}}&{a_{n2}}&{\cdots}&{a_{nn}}\\ \end{bmatrix} \begin{bmatrix} {x_{1}}\\ {x_{2}}\\ {\vdots}\\ {a_{n}}\\ \end{bmatrix} =(x_1, x_2,\cdots, x_n)(\Sigma_{j=1}^{n}{a_{1j}{x_j}}, \Sigma_{j=1}^{n}{a_{2j}{x_j}}, \cdots, \Sigma_{j=1}^{n}{a_{nj}{x_j}})^T =x_1\Sigma_{j=1}^{n}{a_{1j}{x_j}} + x_2\Sigma_{j=1}^{n}{a_{2j}{x_j}} + \cdots + x_n\Sigma_{j=1}^{n}{a_{nj}{x_j}} =\Sigma_{i=1}^{n} \Sigma_{j=1}^{n} a_{ij} x_i x_j$$